Как правильно сравнивать числа с плавающей точкой в Python.
Числа с плавающей точкой — это быстрый и эффективный способ хранения и работы с числами, но они имеют ряд подводных камней, которые наверняка ставят в тупик многих начинающих программистов, а возможно, и опытных! Классический пример, демонстрирующий подводные камни плавающих чисел, выглядит следующим образом:
>>> 0.1 + 0.2 == 0.3 False
Увидев это в первый раз, вы можете быть дезориентированы. Но не выбрасывайте свой компьютер в мусорную корзину. Это правильное поведение!
В этой статье вы узнаете, почему ошибки с плавающей точкой, подобные приведенной выше, встречаются часто, почему они имеют смысл, и что можно сделать, чтобы справиться с ними в Python.
Ваш компьютер — лжец (вроде того)
Вы видели, что 0,1 + 0,2 не равно 0,3, но на этом безумие не заканчивается. Вот еще несколько сбивающих с толку примеров:
>>> 0.2 + 0.2 + 0.2 == 0.6 False >>> 1.3 + 2.0 == 3.3 False >>> 1.2 + 2.4 + 3.6 == 7.2 False
Проблема также не ограничивается сравнением равенства:
>>> 0.1 + 0.2 <= 0.3 False >>> 10.4 + 20.8 > 31.2 True >>> 0.8 - 0.1 > 0.7 True
Так что же происходит? Ваш компьютер обманывает вас? Похоже на то, но под поверхностью происходит нечто большее.
Когда вы вводите число 0.1 в интерпретатор Python, оно сохраняется в памяти как число с плавающей точкой. При этом происходит преобразование. 0,1 — это десятичная дробь по основанию 10, но числа с плавающей точкой хранятся в двоичном формате. Другими словами, 0,1 преобразуется из основания 10 в основание 2.
Полученное двоичное число может не точно представлять исходное число по основанию 10. 0,1 — один из примеров. Двоичное представление 0.000111. То есть, 0,1 является бесконечно повторяющейся десятичной дробью при записи по основанию 2. То же самое происходит, когда вы записываете дробь ⅓ в виде десятичной дроби по основанию 10. В итоге вы получаете бесконечно повторяющуюся десятичную дробь 0.33.
Память компьютера ограничена, поэтому бесконечно повторяющееся двоичное дробное представление 0,1 округляется до конечной дроби. Значение этого числа зависит от архитектуры вашего компьютера (32-битная или 64-битная). Один из способов увидеть значение с плавающей точкой, которое хранится для 0,1, — использовать метод .as_integer_ratio() для плавающих чисел, чтобы получить числитель и знаменатель представления с плавающей точкой:
>>> numerator, denominator = (0.1).as_integer_ratio()
>>> f"0.1 ≈ {numerator} / {denominator}"
'0.1 ≈ 3602879701896397 / 36028797018963968'
Теперь используйте format(), чтобы показать дробь с точностью до 55 знаков после запятой:
>>> format(numerator / denominator, ".55f") '0.1000000000000000055511151231257827021181583404541015625'
Поэтому 0,1 округляется до числа, которое немного больше его истинного значения.
Эта ошибка, известная как ошибка представления с плавающей точкой (floating-point representation error), случается гораздо чаще, чем вы можете себе представить.
Ошибка репрезентативности действительно распространена
Существует три причины, по которым число округляется при представлении в виде числа с плавающей точкой:
- Число имеет больше значащих цифр, чем позволяет плавающая точка.
- Число иррационально.
- Число рационально, но имеет нетерминированное двоичное представление.
64-битные числа с плавающей точкой имеют 16 или 17 значащих цифр. Любое число с большим количеством значащих цифр округляется. Иррациональные числа, такие как π и e, не могут быть представлены ни одной конечной дробью ни в одной целочисленной базе. Поэтому, опять же, несмотря ни на что, иррациональные числа будут округляться при хранении в виде плавающих чисел.
Эти две ситуации создают бесконечное множество чисел, которые нельзя точно представить в виде числа с плавающей запятой. Но если вы не химик, имеющий дело с крошечными числами, или физик, имеющий дело с астрономически большими числами, вы вряд ли столкнетесь с этими проблемами.
А как насчет рациональных чисел без конца, например, 0,1 в основании 2? Именно здесь вы столкнетесь с большинством проблем с плавающей запятой, а благодаря математике, определяющей, заканчивается ли дробь, вы столкнетесь с ошибкой представления чаще, чем вы думаете.
В основании 10 дробь конечна, если ее знаменатель является произведением степеней простых множителей 10.
Два простых множителя 10 это 2 и 5, поэтому дроби ½, ¼, ⅕, ⅛ и ⅒ все конечны, а ⅓, ⅐ и ⅑ — нет. Однако в основании 2 есть только один простой множитель — 2. Поэтому только дроби, знаменатель которых равен степени 2, имеют конечный результат. В результате дроби типа ⅓, ⅕, ⅙, ⅐, ⅑ и ⅒, выраженные в двоичной форме, являются непересекающимися.
Теперь вы можете понять исходный пример в этой статье. 0.1, 0.2 и 0.3 округляются при преобразовании в числа с плавающей точкой:
>>> # -----------vvvv Display with 17 significant digits >>> format(0.1, ".17g") '0.10000000000000001' >>> format(0.2, ".17g") '0.20000000000000001' >>> format(0.3, ".17g") '0.29999999999999999'
При сложении 0,1 и 0,2 получается число, немного большее, чем 0,3:
>>> 0.1 + 0.2 0.30000000000000004
Поскольку 0,1 + 0,2 немного больше, чем 0,3, а 0,3 представляется числом, которое немного меньше его самого, выражение 0,1 + 0,2 == 0,3 имеет значение False.
Как сравнивать плавающие числа в Python
Как же бороться с ошибками представления с плавающей точкой при сравнении плавающих чисел в Python? Хитрость заключается в том, чтобы избежать проверки равенства. Никогда не используйте ==, >= или <= с плавающей точкой. Вместо этого используйте функцию math.isclose():
>>> import math >>> math.isclose(0.1 + 0.2, 0.3) True
math.isclose() проверяет, близок ли первый аргумент ко второму. Но что именно это значит? Основная идея заключается в том, чтобы проверить расстояние между первым и вторым аргументом, которое эквивалентно абсолютному значению разности этих величин:
>>> a = 0.1 + 0.2 >>> b = 0.3 >>> abs(a - b) 5.551115123125783e-17
Если abs(a — b) меньше некоторого процента от большего из a или b, то a считается достаточно близким к b, чтобы быть «равным» b. Этот процент называется относительным допуском.
Вы можете указать относительный допуск с помощью аргумента rel_tol ключевого слова math.isclose(), который по умолчанию равен 1e-9. Другими словами, если abs(a — b) меньше 1e-9 * max(abs(a), abs(b)), то a и b считаются «близкими» друг к другу. Это гарантирует, что a и b равны примерно до девяти знаков после запятой.
При необходимости вы можете изменить относительный допуск:
>>> math.isclose(0.1 + 0.2, 0.3, rel_tol=1e-20) False
Конечно, относительный допуск зависит от ограничений, установленных решаемой вами задачей. Однако для большинства повседневных приложений достаточно относительного допуска по умолчанию.
Однако существует проблема, если одно из a или b равно нулю, а rel_tol меньше единицы. В этом случае, как бы близко ненулевое значение ни было к нулю, относительный допуск гарантирует, что проверка на близость всегда будет неудачной. В этом случае использование абсолютного допуска работает как запасной вариант:
>>> # Relative check fails! >>> # ---------------vvvv Relative tolerance >>> # ----------------------vvvvv max(0, 1e-10) >>> abs(0 - 1e-10) < 1e-9 * 1e-10 False >>> # Absolute check works! >>> # ---------------vvvv Absolute tolerance >>> abs(0 - 1e-10) < 1e-9 True
math.isclose() выполнит эту проверку автоматически. Аргумент ключевого слова abs_tol определяет абсолютный допуск. Однако по умолчанию abs_tol равен 0.0, поэтому вам придется задать его вручную, если вам нужно проверить, насколько близко значение к нулю.
В целом, math.isclose() возвращает результат следующего сравнения, которое объединяет относительный и абсолютный тесты в одно выражение:
abs(a - b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol)
math.isclose() была введена в PEP 485 и доступна с Python 3.5.
Когда следует использовать math.isclose()?
В целом, следует использовать math.isclose() всякий раз, когда вам нужно сравнить значения с плавающей точкой. Замените == на math.isclose():
>>> # Don't do this: >>> 0.1 + 0.2 == 0.3 False >>> # Do this instead: >>> math.isclose(0.1 + 0.2, 0.3) True
Также нужно быть осторожным со сравнениями >= и <=. Обработайте равенство отдельно с помощью math.isclose(), а затем проверьте строгое сравнение:
>>> a, b, c = 0.1, 0.2, 0.3 >>> # Don't do this: >>> a + b <= c False >>> # Do this instead: >>> math.isclose(a + b, c) or (a + b < c) True
Существуют различные альтернативы math.isclose(). Если вы используете NumPy, вы можете использовать numpy.allclose() и numpy.isclose():
>>> import numpy as np >>> # Use numpy.allclose() to check if two arrays are equal >>> # to each other within a tolerance. >>> np.allclose([1e10, 1e-7], [1.00001e10, 1e-8]) False >>> np.allclose([1e10, 1e-8], [1.00001e10, 1e-9]) True >>> # Use numpy.isclose() to check if the elements of two arrays >>> # are equal to each other within a tolerance >>> np.isclose([1e10, 1e-7], [1.00001e10, 1e-8]) array([ True, False]) >>> np.isclose([1e10, 1e-8], [1.00001e10, 1e-9]) array([ True, True])
Имейте в виду, что относительные и абсолютные допуски по умолчанию не совпадают с math.isclose(). Относительный допуск по умолчанию для numpy.allclose() и numpy.isclose() равен 1e-05, а абсолютный допуск по умолчанию для обоих вариантов равен 1e-08.
Метод math.isclose() особенно полезен для модульных тестов, хотя есть и альтернативы. Встроенный в Python модуль unittest имеет метод unittest.TestCase.assertAlmostEqual(). Однако этот метод использует только тест на абсолютное различие. Кроме того, это утверждение, а значит, при сбоях возникает ошибка AssertionError, что делает его непригодным для сравнений в вашей бизнес-логике.
Отличной альтернативой math.isclose() для модульного тестирования является функция pytest.approx() из пакета pytest. В отличие от math.isclose(), pytest.approx() принимает только один аргумент — ожидаемое значение:
>>> import pytest >>> 0.1 + 0.2 == pytest.approx(0.3) True
pytest.approx() имеет ключевые аргументы rel_tol и abs_tol для установки относительных и абсолютных допусков. Однако значения по умолчанию отличаются от math.isclose(). rel_tol по умолчанию имеет значение 1e-6, а abs_tol по умолчанию имеет значение 1e-12.
Если аргумент, переданный в pytest.approx(), является массивоподобным, то есть это итерабельность Python, например, список или кортеж, или даже массив NumPy, то pytest.approx() ведет себя аналогично numpy.allclose() и возвращает, равны ли два массива в пределах допусков:
>>> import numpy as np >>> np.array([0.1, 0.2]) + np.array([0.2, 0.4]) == pytest.approx(np.array([0.3, 0.6])) True
pytest.approx() будет работать даже со словарными значениями:
>>> {'a': 0.1 + 0.2, 'b': 0.2 + 0.4} == pytest.approx({'a': 0.3, 'b': 0.6})
True
Числа с плавающей точкой отлично подходят для работы с числами, когда не требуется абсолютная точность. Они быстрые и занимают мало памяти. Но если вам нужна точность, то следует рассмотреть некоторые альтернативы плавающим числам.
Точные альтернативы с плавающей точкой
В Python есть два встроенных числовых типа, которые обеспечивают полную точность в ситуациях, когда плавающие числа не подходят: Decimal и Fraction.
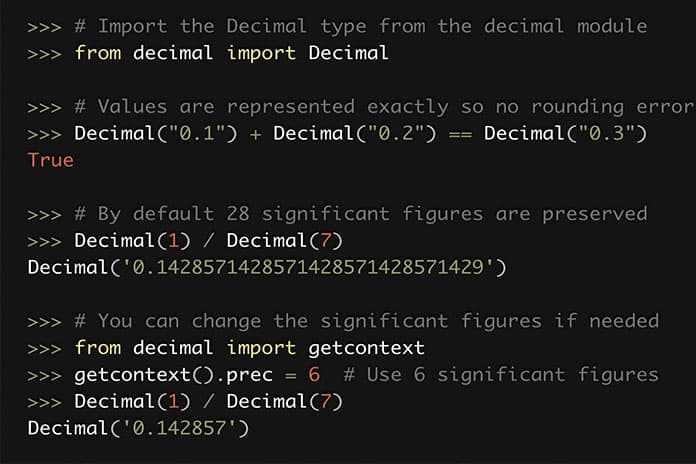
Тип Decimal может хранить десятичные значения с той точностью, которая вам необходима. По умолчанию Decimal сохраняет 28 значащих цифр, но вы можете изменить это значение на любое необходимое для решения конкретной задачи:
>>> # Import the Decimal type from the decimal module
>>> from decimal import Decimal
>>> # Values are represented exactly so no rounding error occurs
>>> Decimal("0.1") + Decimal("0.2") == Decimal("0.3")
True
>>> # By default 28 significant figures are preserved
>>> Decimal(1) / Decimal(7)
Decimal('0.1428571428571428571428571429')
>>> # You can change the significant figures if needed
>>> from decimal import getcontext
>>> getcontext().prec = 6 # Use 6 significant figures
>>> Decimal(1) / Decimal(7)
Decimal('0.142857')
Подробнее о типе Decimal можно прочитать в документации Python.
Тип дроби
Другой альтернативой числам с плавающей точкой является тип Fraction. Дробь может точно хранить рациональные числа и преодолевает проблемы ошибок представления, с которыми сталкиваются числа с плавающей точкой:
>>> # import the Fraction type from the fractions module >>> from fractions import Fraction >>> # Instantiate a Fraction with a numerator and denominator >>> Fraction(1, 10) Fraction(1, 10) >>> # Values are represented exactly so no rounding error occurs >>> Fraction(1, 10) + Fraction(2, 10) == Fraction(3, 10) True
Дробные и десятичные числа обладают многочисленными преимуществами по сравнению со стандартными значениями с плавающей точкой. Однако за эти преимущества приходится платить: снижение скорости и увеличение потребления памяти. Если вам не нужна абсолютная точность, лучше остановиться на плавающей точке. Но для таких задач, как финансовые и критически важные приложения, компромисс между дробью и десятичной дробью может оказаться оправданным.
Заключение
Значения с плавающей точкой — это одновременно и преимущество, и недостаток. Они обеспечивают быстрое выполнение арифметических операций и эффективное использование памяти ценой неточного представления. В этой статье вы узнали:
- Почему числа с плавающей точкой являются неточными
- Почему часто встречаются ошибки представления чисел с плавающей точкой
- Как правильно сравнивать значения с плавающей точкой в Python
- Как точно представлять числа с помощью типов Python Fraction и Decimal
Возможно вам будет интересно:
Алгоритмы сортировки 26 видов
Алгоритмы и структуры данных на Python
100+ сложных упражнений по программированию на Python