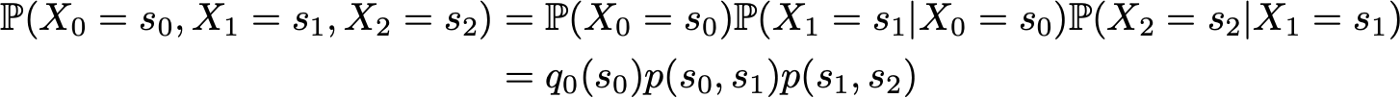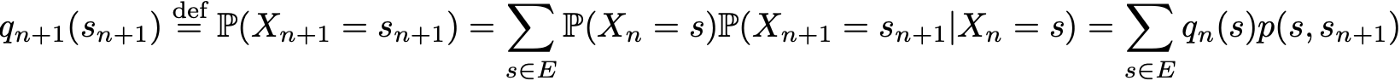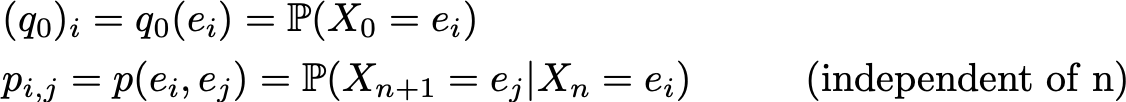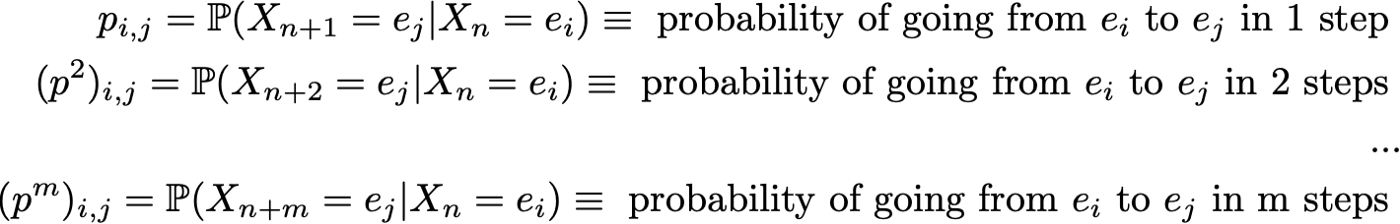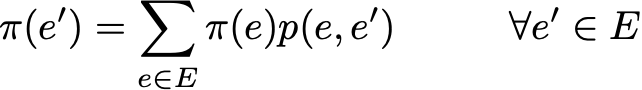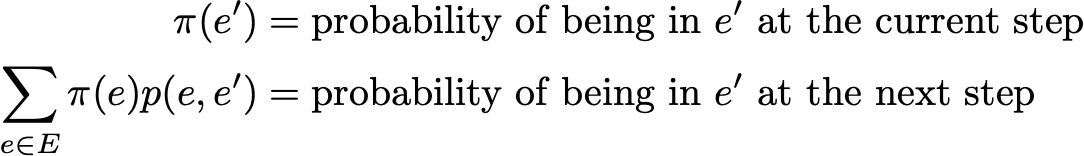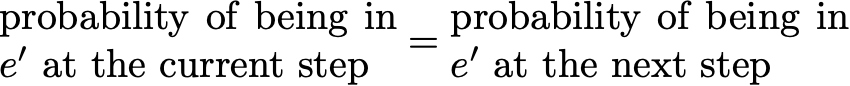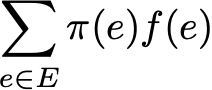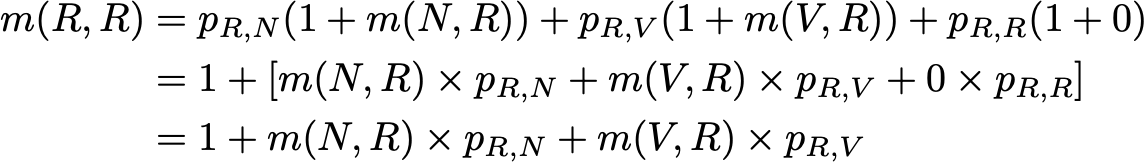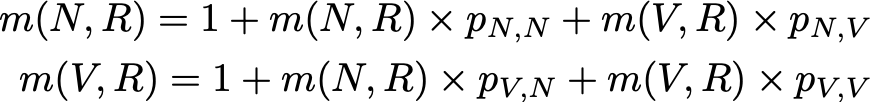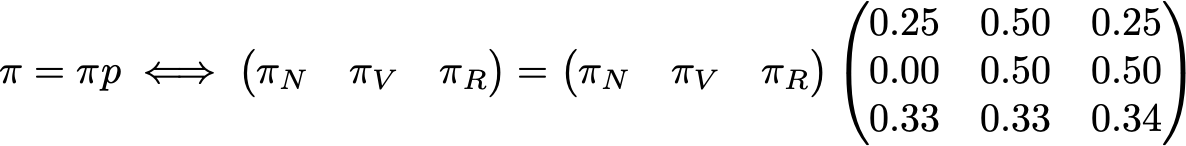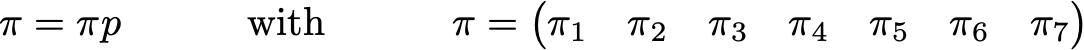Цепи Маркова, определения, свойства и пример PageRank.
Введение
В 1998 году Лоуренс Пейдж, Сергей Брин, Раджив Мотвани и Терри Виноград опубликовали статью «Рейтинг цитирования PageRank: Bringing Order to the Web», статью, в которой они представили ныне известный алгоритм PageRank, стоящий у истоков Google. Прошло чуть больше двух десятилетий, Google стал гигантом, и, несмотря на то, что алгоритм претерпел значительные изменения, PageRank по-прежнему является «символом» алгоритма ранжирования Google (хотя мало кто может сказать, какое место он занимает в алгоритме).
С теоретической точки зрения интересно отметить, что одна из распространенных интерпретаций алгоритма PageRank опирается на простое, но фундаментальное математическое понятие цепей Маркова. В этой статье мы увидим, что цепи Маркова — это мощный инструмент стохастического моделирования, который может быть полезен любому специалисту по исследованию данных. В частности, мы ответим на такие основные вопросы, как: что такое цепи Маркова, какими хорошими свойствами они обладают и что с ними можно делать?
Краткое описание
В первом разделе мы дадим основные определения, необходимые для понимания того, что такое цепи Маркова. Во втором разделе мы обсудим особый случай марковских цепей в конечном пространстве состояний. Затем, в третьем разделе мы обсудим некоторые элементарные свойства цепей Маркова и проиллюстрируем эти свойства множеством небольших примеров. Наконец, в четвертом разделе мы установим связь с алгоритмом PageRank и рассмотрим на условном примере, как цепи Маркова могут быть использованы для ранжирования узлов графа.
Примечание. В этом посте требуются основы вероятности и линейной алгебры. В частности, будут использованы следующие понятия: условная вероятность, собственный вектор и закон полной вероятности.
Что такое цепи Маркова?
Случайные величины и случайные процессы
Прежде чем представить цепи Маркова, давайте начнем с краткого напоминания некоторых основных, но важных понятий теории вероятностей.
Во-первых, в нематематических терминах, случайная величина X — это переменная, значение которой определяется как результат случайного явления. Этот результат может быть числом (или «числоподобным», включая векторы) или нет. Например, мы можем определить случайную переменную как результат броска игральной кости (число), а также как результат подбрасывания монеты (не число, если, например, не присвоить 0 головке и 1 решке). Обратите внимание, что пространство возможных исходов случайной величины может быть дискретным или непрерывным: например, нормальная случайная величина является непрерывной, тогда как пуассоновская случайная величина является дискретной
Затем мы можем определить случайный процесс (также называемый стохастическим процессом) как набор случайных величин, индексируемых множеством T, которые часто представляют различные моменты времени (в дальнейшем мы будем исходить из этого). Наиболее распространены два случая: либо T — множество натуральных чисел (случайный процесс с дискретным временем), либо T — множество вещественных чисел (случайный процесс с непрерывным временем). Например, ежедневное подбрасывание монеты определяет дискретный случайный процесс, в то время как цена опциона на фондовом рынке, изменяющаяся непрерывно, определяет непрерывный случайный процесс. Случайные величины в разные моменты времени могут быть независимы друг от друга (пример с подбрасыванием монетки) или зависимы каким-либо образом (пример с ценой акций), а также могут иметь непрерывное или дискретное пространство состояний (пространство возможных исходов в каждый момент времени)..
Свойство Маркова и цепь Маркова
Существует несколько хорошо известных семейств случайных процессов: гауссовы процессы, процессы Пуассона, модели авторегрессии, модели скользящего среднего, цепи Маркова и другие. Каждый из этих частных случаев обладает специфическими свойствами, которые позволяют нам лучше изучить и понять их.
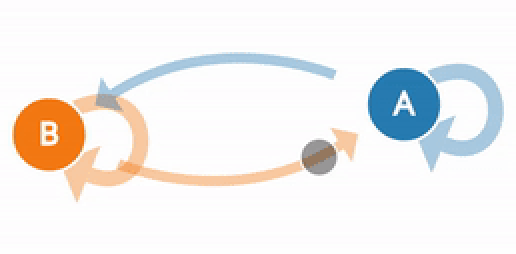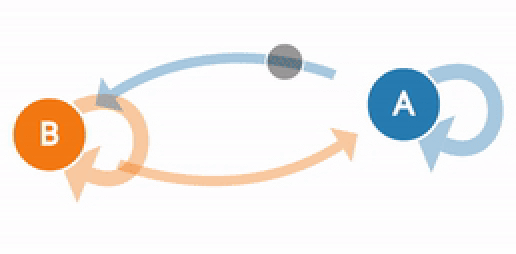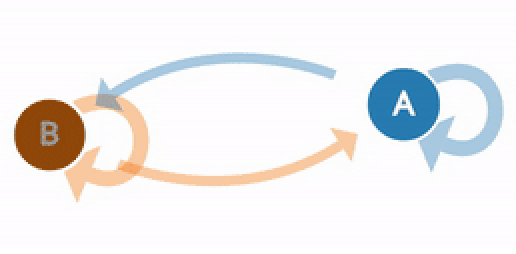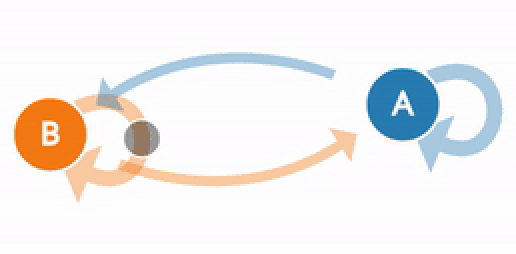
Одно из свойств, которое значительно упрощает изучение случайного процесса, — это «свойство Маркова». В очень неформальном виде свойство Маркова говорит для случайного процесса, что если мы знаем значение, которое принимает процесс в данный момент времени, то мы не получим никакой дополнительной информации о будущем поведении процесса, если соберем больше знаний о прошлом. Говоря более математическим языком, для любого данного времени условное распределение будущих состояний процесса с учетом настоящего и прошлого состояний зависит только от настоящего состояния и совсем не зависит от прошлого (свойство беспамятности). Случайный процесс, обладающий свойством Маркова, называется марковским процессом.
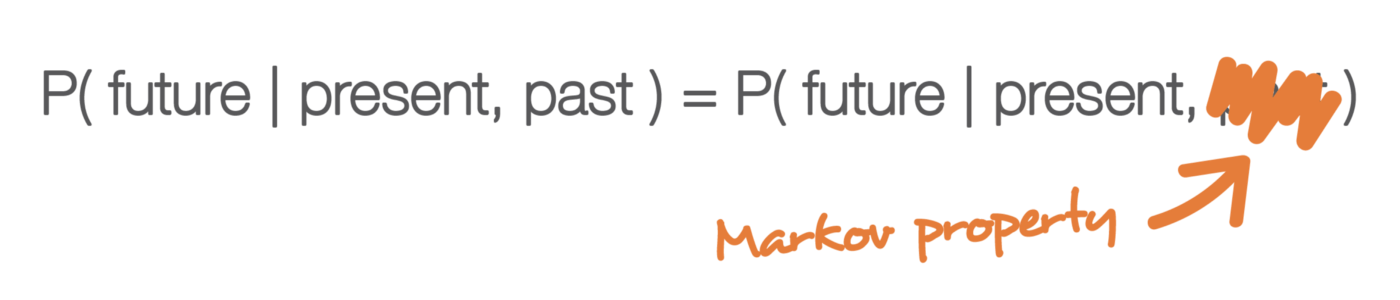
Исходя из предыдущего определения, мы можем теперь определить «однородные цепи Маркова дискретного времени» (которые для простоты в дальнейшем будут обозначаться «цепями Маркова»). Цепь Маркова — это марковский процесс с дискретным временем и дискретным пространством состояний. Таким образом, цепь Маркова — это дискретная последовательность состояний, каждое из которых берется из дискретного пространства состояний (конечного или нет), и которая следует свойству Маркова.
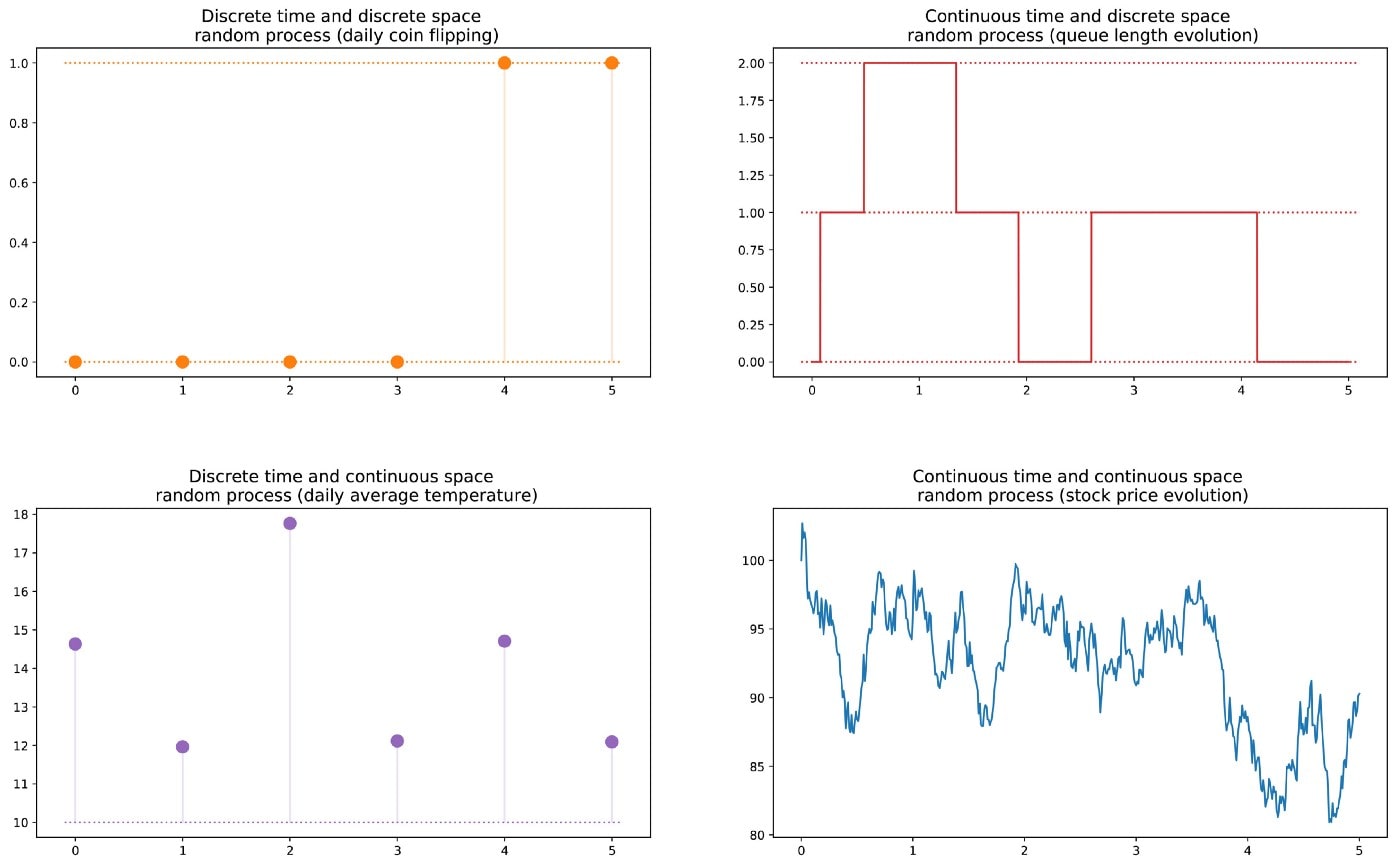
Математически мы можем обозначить цепь Маркова через
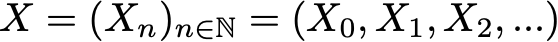
где в каждый момент времени процесс принимает свои значения в дискретном множестве E такие, что
Тогда из свойства Маркова следует, что мы имеем
Заметьте еще раз, что эта последняя формула выражает тот факт, что для данного исторического состояния (где я сейчас и где я был раньше), распределение вероятности для следующего состояния (куда я пойду дальше) зависит только от текущего состояния, но не от прошлых состояний.
Примечание. Мы решили описать только основные однородные дискретные временные цепи Маркова в этой вводной статье. Однако существуют также неоднородные (зависящие от времени) и/или непрерывные во времени цепи Маркова. В дальнейшем мы не будем обсуждать эти варианты модели. Заметьте также, что определение свойства Маркова, данное выше, является крайне упрощенным: истинное математическое определение включает в себя понятие фильтрации, которое выходит далеко за рамки этого скромного введения.
Характеристика случайной динамики цепи Маркова
В предыдущем подразделе мы представили общие рамки, которым соответствует любая цепь Маркова. Теперь посмотрим, что нам нужно для определения конкретного «экземпляра» такого случайного процесса.
Заметим сначала, что полная характеристика случайного процесса с дискретным временем, не удовлетворяющего свойству Маркова, может быть болезненной: распределение вероятностей в данный момент времени может зависеть от одного или нескольких моментов времени в прошлом и/или будущем. Все эти возможные зависимости от времени делают любое правильное описание процесса потенциально сложным.
Однако, благодаря свойству Маркова, динамику цепи Маркова довольно легко определить. Действительно, нам нужно указать только две вещи: начальное распределение вероятностей (то есть распределение вероятностей для момента времени n=0), обозначаемое
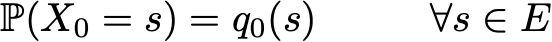
и ядро вероятностей перехода (которое дает вероятности того, что состояние в момент времени n+1 переходит в другое состояние в момент времени n для любой пары состояний), обозначаемое
Когда два предыдущих объекта известны, полная (вероятностная) динамика процесса хорошо определена. Действительно, вероятность любой реализации процесса может быть вычислена рекуррентным способом.
Предположим, например, что мы хотим знать вероятность того, что первые 3 состояния процесса будут (s0, s1, s2). Таким образом, мы хотим вычислить вероятность
Здесь мы используем закон полной вероятности, который гласит, что вероятность того, что мы имеем (s0, s1, s2), равна вероятности того, что мы имеем сначала s0, умноженной на вероятность того, что мы имеем s1, учитывая, что до этого мы имели s0, умноженной на вероятность того, что, наконец, мы имеем s2, учитывая, что до этого мы имели по порядку s0 и s1. Математически это можно записать так
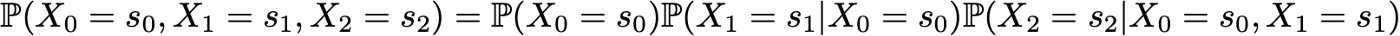
Тогда возникает упрощение, обусловленное предположением Маркова. Действительно, для длинных цепей мы получили бы для последних состояний сильно выраженные условные вероятности. Однако в марковском случае мы можем упростить это выражение, используя
и что мы имеем
Поскольку они полностью характеризуют вероятностную динамику процесса, многие другие более сложные события могут быть вычислены только на основе начального распределения вероятности q0 и ядра вероятности перехода p. Последнее основное отношение, которое заслуживает быть приведенным, это выражение распределения вероятности в момент времени n+1, выраженное относительно распределения вероятности в момент времени n
Марковские цепи в конечном пространстве состояний
Матричное и графовое представление
Здесь мы предполагаем, что у нас есть конечное число N возможных состояний в E:
Тогда начальное распределение вероятностей может быть описано вектором строк q0 размера N, а вероятности перехода могут быть описаны матрицей p размера N на N, такой, что
Преимущество такой нотации состоит в том, что если мы обозначим распределение вероятностей на шаге n с помощью исходного вектора qn так, что его компоненты задаются
то после этого выполняются простые матричные соотношения
(доказательство не будет здесь подробно описано, но его можно легко найти).
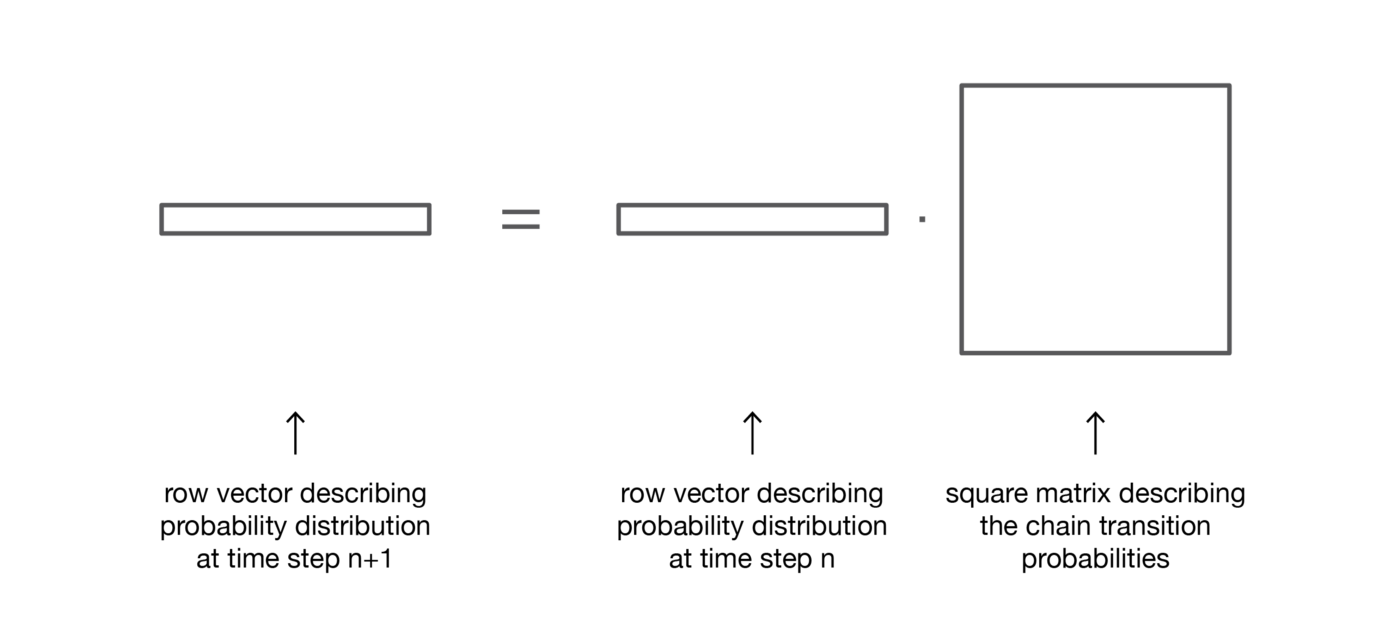
Таким образом, мы видим, что эволюция распределения вероятностей от данного шага к последующему так же проста, как умножение вектора вероятностей строки начального шага на матрицу p. Из этого также следует, что мы имеем
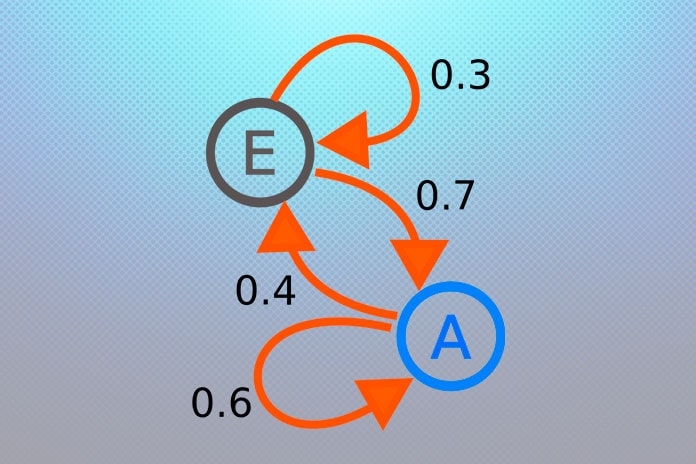
Случайная динамика марковской цепи с конечным пространством состояний может быть легко представлена в виде ориентированного графа, где каждый узел графа — это состояние, и для всех пар состояний (ei, ej) существует ребро, идущее от ei к ej, если p(ei,ej)>0. Тогда значение ребра равно этой самой вероятности p(ei,ej).
Пример: читатель Towards Data Science
Давайте возьмем простой пример, чтобы проиллюстрировать все это. Рассмотрим повседневное поведение вымышленного читателя по отношению к науке о данных. Для каждого дня существует 3 возможных состояния: читатель не посещает TDS в этот день (N), читатель посещает TDS, но не читает полный пост (V) и читатель посещает TDS и прочитал хотя бы один полный пост (R). Итак, у нас есть следующее пространство состояний
Предположим, что в первый день этот читатель имеет 50% шансов только посетить TDS и 50% шансов посетить TDS и прочитать хотя бы одну статью. Тогда вектор, описывающий начальное распределение вероятностей (n=0), имеет вид
Представьте также, что наблюдаются следующие вероятности:
- когда читатель не посещает TDS в день, у него есть 25% шансов не посетить его на следующий день, 50% шансов только посетить и 25% посетить и прочитать
- когда читатель посещает TDS без чтения в день, у него есть 50% шансов снова посетить без чтения на следующий день и 50% — посетить и прочитать
- когда читатель посещает и читает один день, у него есть 33% шансов не посетить сайт на следующий день (надеюсь, что этот пост не будет иметь такого эффекта!), 33% шансов только посетить и 34% посетить и прочитать снова
Тогда мы имеем следующую матрицу перехода
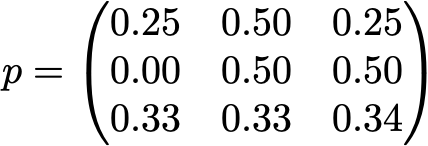
Исходя из предыдущего подраздела, мы знаем, как вычислить для этого читателя вероятность каждого состояния для второго дня (n=1)
Наконец, вероятностная динамика этой цепи Маркова может быть представлена графически следующим образом
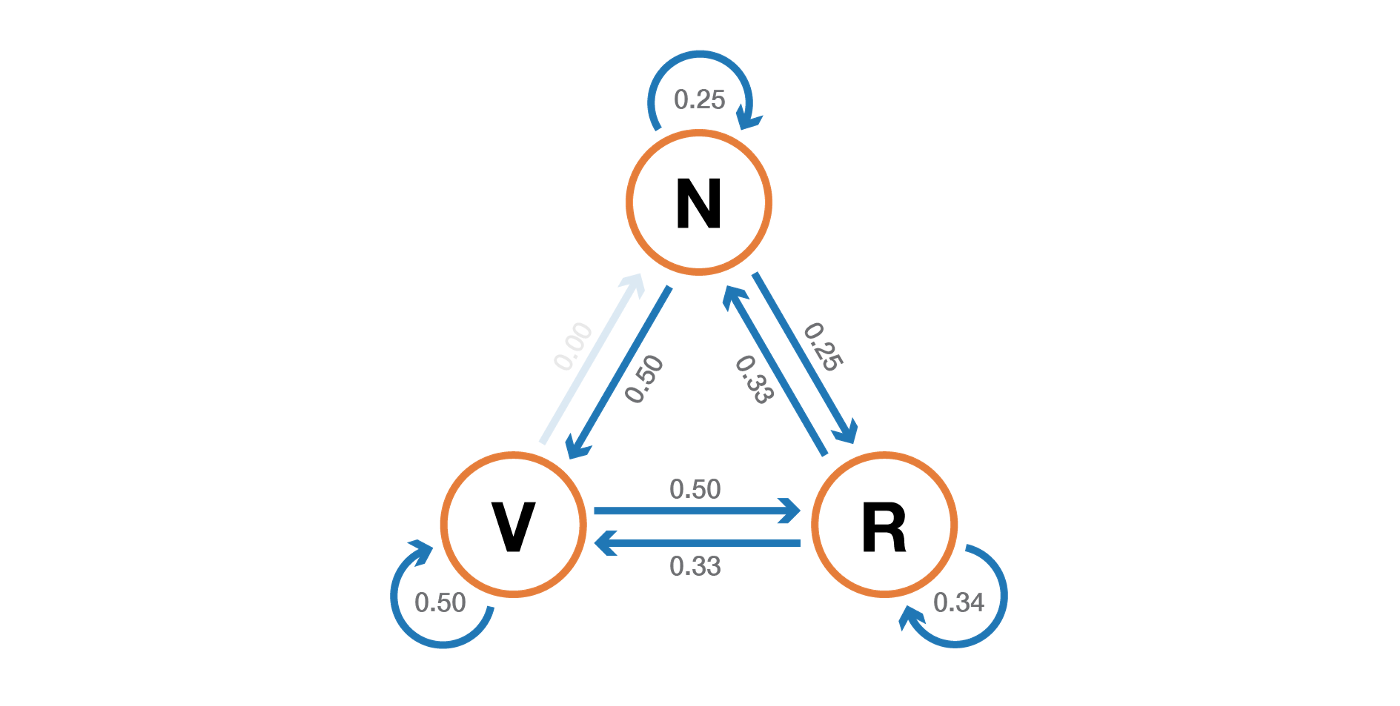
Свойства цепей Маркова
В этом разделе мы приведем только некоторые основные свойства или характеристики цепей Маркова. Идея состоит в том, чтобы не углубляться в математические детали, а дать общее представление о том, какие моменты, представляющие интерес, необходимо изучить при использовании цепей Маркова. Поскольку мы видели, что в случае конечного пространства состояний мы можем представить цепь Маркова в виде графа, обратите внимание, что мы будем использовать графическое представление для иллюстрации некоторых свойств, описанных ниже. Однако следует помнить, что эти свойства не обязательно ограничиваются случаем конечного пространства состояний.
Изменяемость, периодичность, переходность и рекуррентность
Начнем в этом подразделе с некоторых классических способов охарактеризовать состояние или всю цепь Маркова.
Во-первых, мы говорим, что цепь Маркова является несводимой, если из любого состояния можно достичь любого другого состояния (не обязательно за один шаг по времени). Если пространство состояний конечное и цепь может быть представлена графом, то можно сказать, что граф несводимой цепи Маркова сильно связный (теория графов).
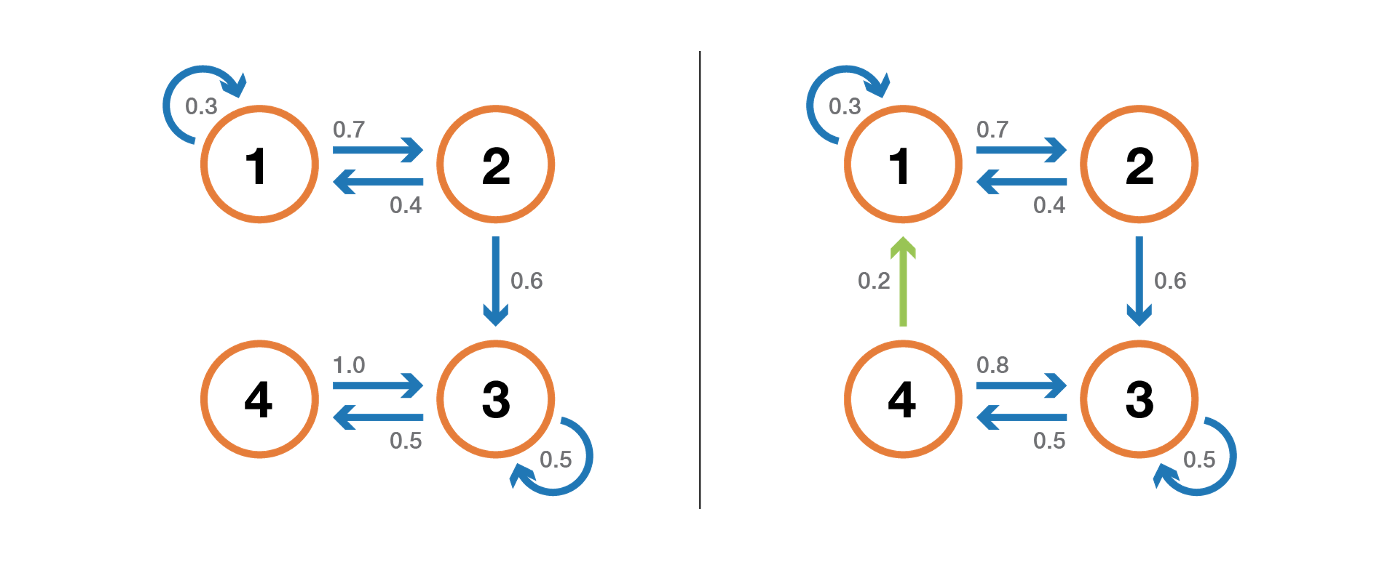
Состояние имеет период k, если при выходе из него любое возвращение в это состояние требует кратного k временных шагов (k — наибольший общий делитель всех возможных длин путей возврата). Если k = 1, то состояние называется апериодическим, а вся цепь Маркова апериодической, если все ее состояния апериодические. Для нередуцируемой цепи Маркова можно также отметить тот факт, что если одно состояние апериодично, то все состояния апериодичны.
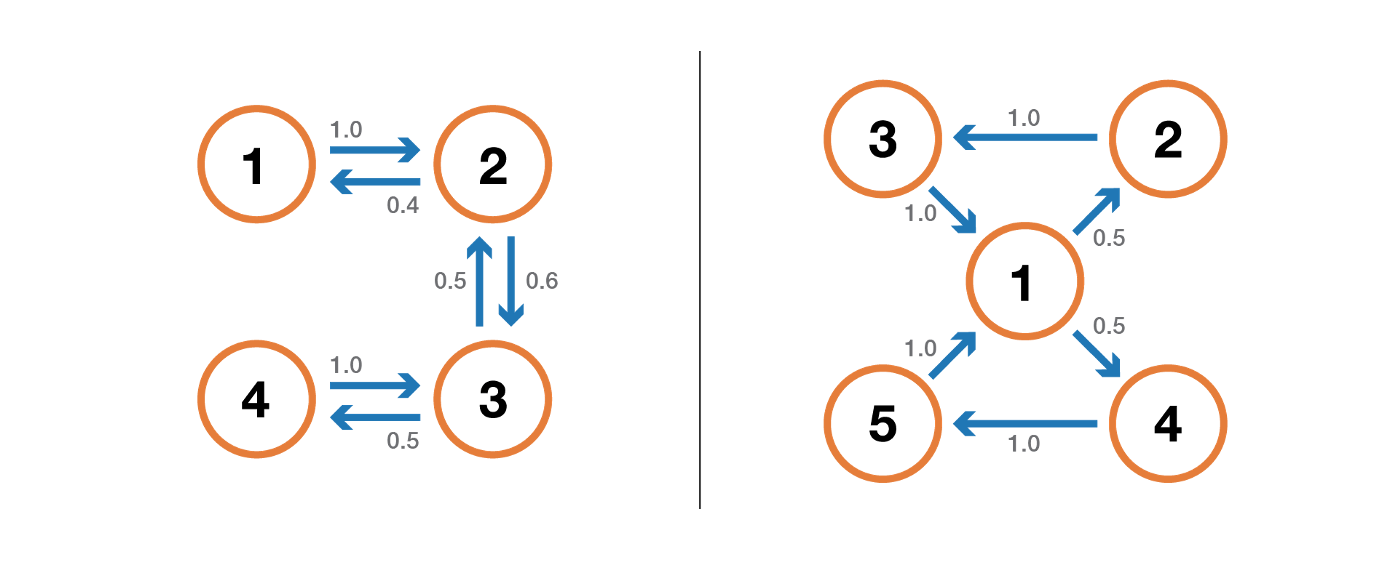
Состояние является переходным, если, когда мы покидаем это состояние, существует ненулевая вероятность того, что мы никогда в него не вернемся. И наоборот, состояние является повторяющимся, если мы знаем, что вернемся в это состояние в будущем с вероятностью 1 после выхода из него (если оно не является переходным).
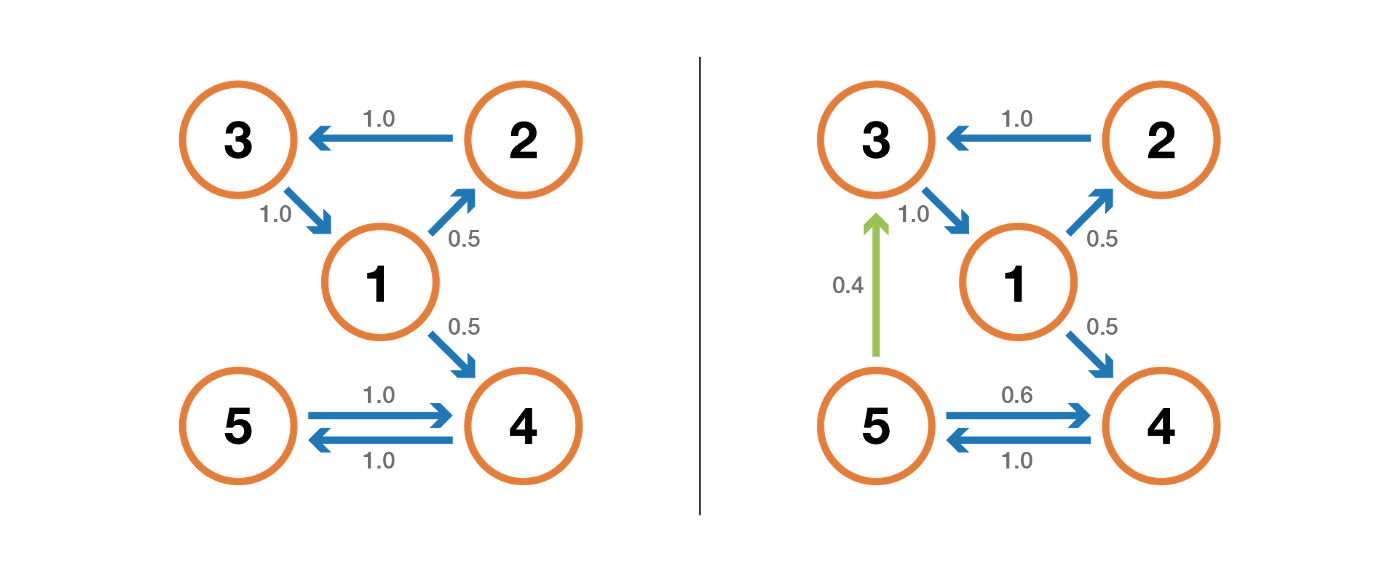
Для повторяющегося состояния мы можем вычислить среднее время повторения, которое является ожидаемым временем возвращения при выходе из состояния. Обратите внимание, что даже если вероятность возвращения равна 1, это не означает, что ожидаемое время возвращения конечное. Таким образом, среди рекуррентных состояний мы можем провести различие между положительным рекуррентным состоянием (конечное ожидаемое время возврата) и нулевым рекуррентным состоянием (бесконечное ожидаемое время возврата).
Стационарное распределение, предельное поведение и эргодичность
В этом подразделе мы обсудим свойства, которые характеризуют некоторые аспекты (случайной) динамики, описываемой цепью Маркова.
Распределение вероятностей на пространстве состояний E называется стационарным, если оно удовлетворяет следующим требованиям
мы имеем
Тогда стационарное распределение подтверждает
По определению, стационарное распределение вероятности таково, что оно не изменяется во времени. Таким образом, если начальное распределение q является стационарным, то оно будет оставаться неизменным для всех будущих временных шагов. Если пространство состояний конечное, p может быть представлено матрицей, а — необработанным вектором, и тогда мы имеем
Это еще раз выражает тот факт, что стационарное распределение вероятности не эволюционирует во времени (как мы видели, правильное умножение распределения вероятности на p позволяет вычислить распределение вероятности на следующем временном шаге). Заметим, что несводимая цепь Маркова имеет стационарное распределение вероятности тогда и только тогда, когда все ее состояния положительно рекуррентны.
Еще одно интересное свойство, связанное со стационарным распределением вероятностей, заключается в следующем. Если цепь рекуррентно положительна (так что существует стационарное распределение) и апериодична, то, независимо от того, каковы начальные вероятности, распределение вероятностей цепи сходится при бесконечном числе шагов по времени: говорят, что цепь имеет предельное распределение, которое есть не что иное, как стационарное распределение. В общем случае это можно записать так
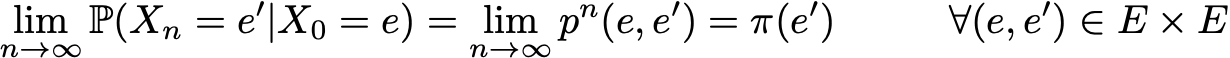
Еще раз подчеркнем тот факт, что нет никаких предположений о начальном распределении вероятностей: распределение вероятностей цепи сходится к стационарному распределению (равновесному распределению цепи) независимо от начальной настройки.
Наконец, эргодичность — это еще одно интересное свойство, связанное с поведением цепи Маркова. Если цепь Маркова несводима, то мы также говорим, что эта цепь «эргодическая», поскольку она подтверждает следующую эргодическую теорему. Предположим, что у нас есть приложение f(.), которое переходит из пространства состояний E на вещественную прямую (это может быть, например, стоимость пребывания в каждом состоянии). Мы можем определить среднее значение, которое берет это приложение по заданной траектории (временное среднее). Для n-го первого члена оно обозначается через
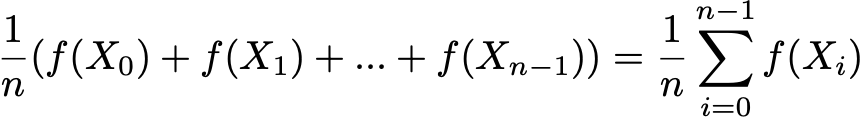
Мы также можем вычислить среднее значение приложения f на множестве E, взвешенное по стационарному распределению (пространственному среднему), которое обозначается как
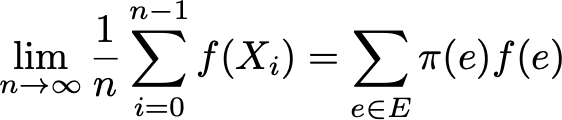
Говоря иначе, это означает, что в пределе раннее поведение траектории становится незначительным, и только долгосрочное стационарное поведение действительно имеет значение при вычислении временного среднего.
Вернемся к нашему примеру с читателем TDS
Мы снова рассмотрим наш пример с читателем TDS. В этом простом примере цепочка явно нередуцируема, апериодична и все состояния рекуррентно положительны.
Чтобы показать, какие интересные результаты можно вычислить с помощью цепей Маркова, мы хотим посмотреть на среднее время повторения для состояния R (состояние «посещение и чтение»). Другими словами, мы хотим ответить на следующий вопрос: когда наш читатель TDS посещает и читает в определенный день, сколько дней в среднем нам придется ждать, прежде чем он посетит и прочитает снова? Давайте попробуем понять, как вычислить это значение.
Во-первых, обозначим
Поэтому мы хотим вычислить здесь m(R,R). Рассуждая о первом шаге, достигнутом после выхода из R, получаем
Это выражение, однако, требует знания m(N,R) и m(V,R) для вычисления m(R,R). Эти две величины могут быть выражены одинаково
Итак, у нас есть 3 уравнения с 3 неизвестными, и, решая эту систему, мы получаем m(N,R) = 2,67, m(V,R) = 2,00 и m(R,R) = 2,54. Тогда значение среднего времени повторения состояния R равно 2,54. Итак, мы видим, что с помощью нескольких элементов линейной алгебры нам удалось вычислить среднее время повторения для состояния R (а также среднее время перехода от N к R и среднее время перехода от V к R).
Чтобы завершить этот пример, давайте посмотрим, каково стационарное распределение этой цепи Маркова. Чтобы определить стационарное распределение, мы должны решить следующее уравнение линейной алгебры
Таким образом, мы должны найти левый собственный вектор p, связанный с собственным значением 1. Решив эту задачу, мы получим следующее стационарное распределение
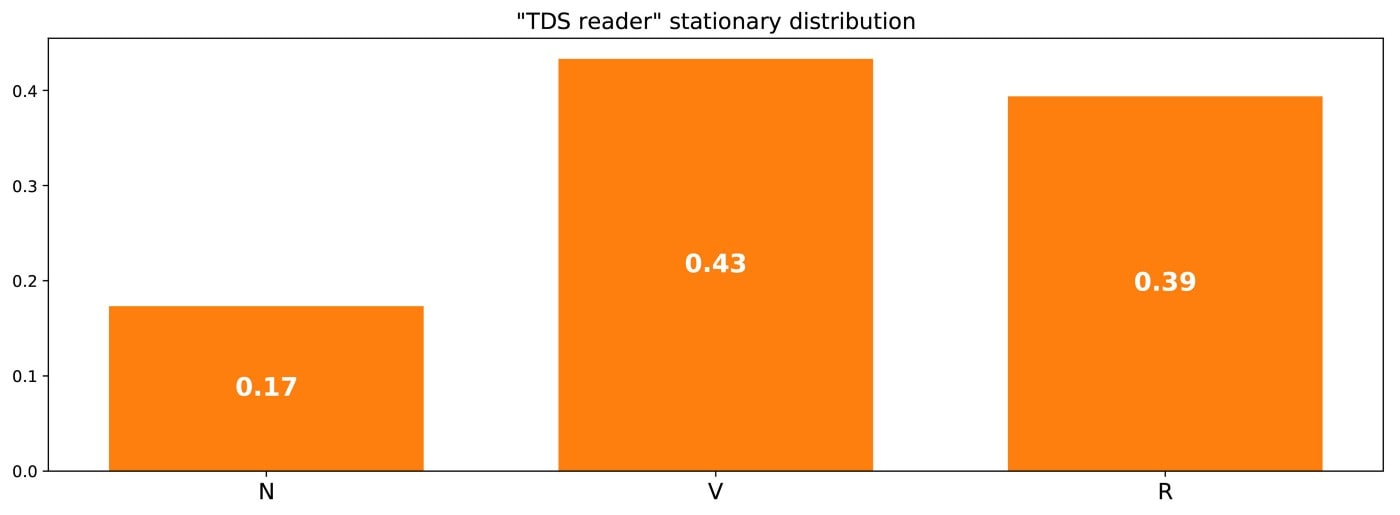
Мы также можем заметить тот факт, что (R) = 1/m(R,R), что является довольно логичным тождеством, если немного подумать об этом (но мы не будем давать больше деталей в этом посте).
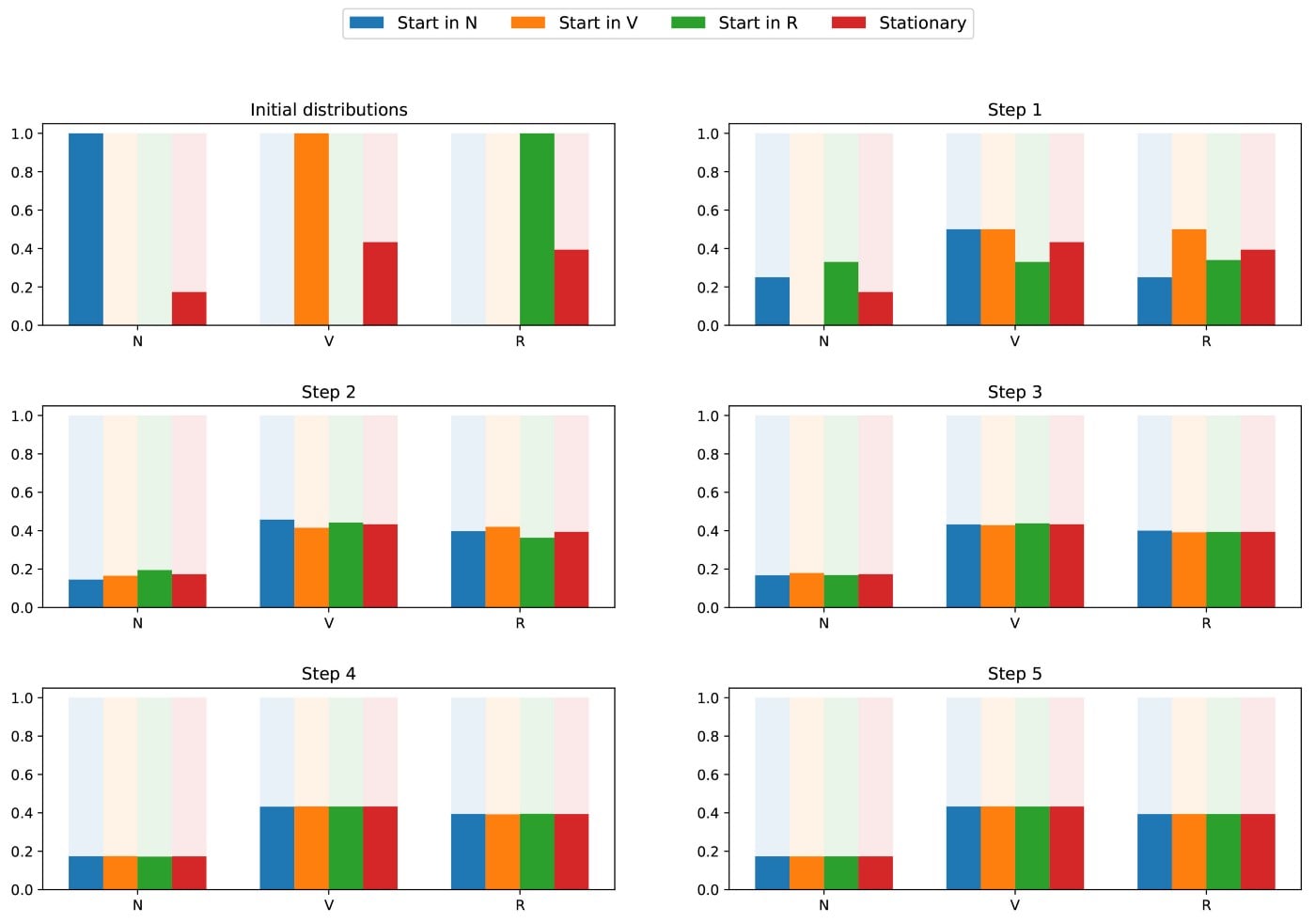
Поскольку цепочка является несводимой и апериодической, это означает, что в долгосрочной перспективе распределение вероятностей будет сходиться к стационарному распределению (при любой инициализации). Говоря иначе, независимо от начального состояния нашего читателя TDS, если мы подождем достаточно долго и выберем день случайным образом, то у нас есть вероятность (N), что читатель не посетит этот день, вероятность (V), что читатель посетит, но не прочитает, и вероятность (R), что читатель посетит и прочитает. Чтобы лучше понять это свойство сходимости, давайте посмотрим на следующий график, который показывает эволюцию распределений вероятностей, начинающихся в разных начальных точках, и (быструю) сходимость к стационарному распределению
Классический пример: алгоритм PageRank
Настало время вернуться к PageRank! Прежде чем продолжить, отметим, что интерпретация, которую мы собираемся дать для PageRank, не является единственно возможной, и что авторы оригинальной статьи не обязательно имели в виду цепи Маркова при разработке метода. Тем не менее, следующая интерпретация имеет большое преимущество — она очень хорошо понятна.
Случайный интернет-пользователь
Проблема, которую пытается решить PageRank, заключается в следующем: как можно ранжировать страницы заданного множества (можно предположить, что это множество уже было отфильтровано, например, по какому-то запросу), используя существующие между ними связи?
Чтобы решить эту проблему и иметь возможность ранжировать страницы, PageRank работает примерно следующим образом. Мы считаем, что случайный интернет-пользователь находится на одной из страниц в начальный момент времени. Затем он начинает случайную навигацию, нажимая для каждой страницы на одну из ссылок, ведущих на другую страницу из рассматриваемого множества (предполагается, что ссылки на страницы из этого множества запрещены). Для данной страницы все разрешенные ссылки имеют равные шансы быть нажатыми.
Мы имеем здесь постановку цепи Маркова: страницы — это различные возможные состояния, вероятности перехода определяются связями от страницы к странице (взвешенными так, что на каждой странице все связанные страницы имеют равные шансы быть выбранными), а свойства отсутствия памяти четко подтверждаются поведением пользователя. Если мы также предположим, что определенная цепочка является рекуррентной положительной и апериодической (для обеспечения этого условия используются некоторые небольшие хитрости), то через длительное время распределение вероятности «текущей страницы» сходится к стационарному распределению. Таким образом, независимо от начальной страницы, через длительное время каждая страница имеет вероятность (почти фиксированную) быть текущей страницей, если мы выберем случайный шаг по времени.
Гипотеза, лежащая в основе PageRank, заключается в том, что наиболее вероятные страницы в стационарном распределении должны быть также наиболее важными (мы часто посещаем эти страницы, потому что они получают ссылки со страниц, которые также часто посещаются в процессе работы). Стационарное распределение вероятностей определяет для каждого состояния значение PageRank.
Пример
Чтобы все это стало намного понятнее, давайте рассмотрим пример. Предположим, что у нас есть маленький сайт с 7 страницами, обозначенными от 1 до 7, со ссылками между страницами, как показано на следующем графике.
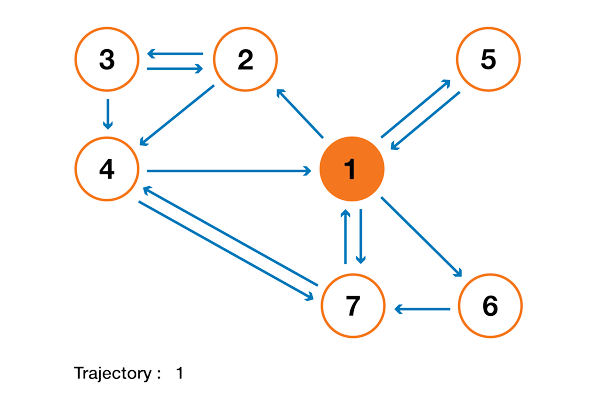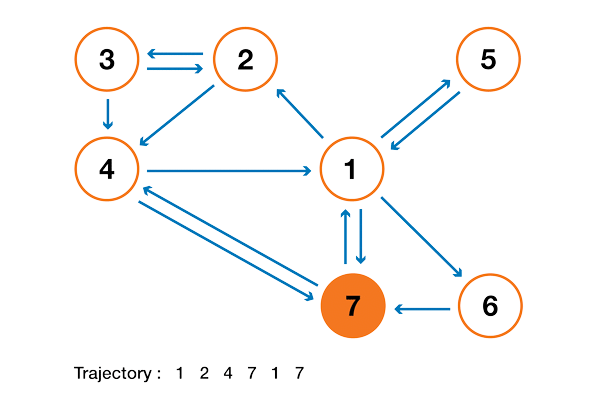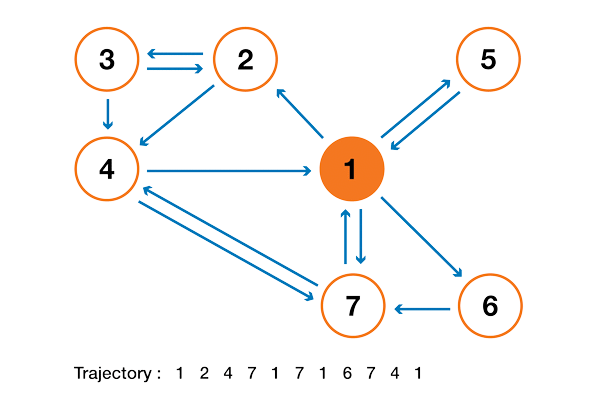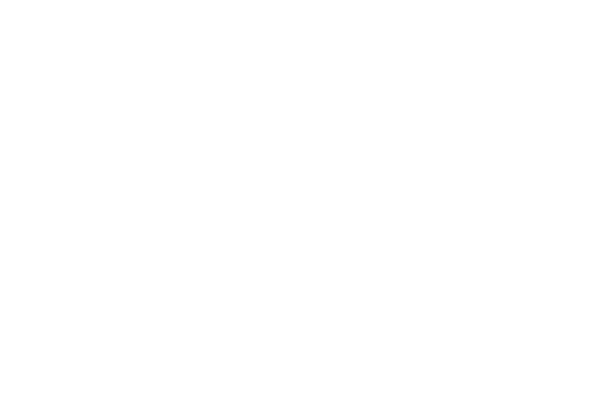
Для наглядности вероятности каждого перехода не были показаны в предыдущем представлении. Однако, поскольку «навигация» предполагается чисто случайной (мы также говорим о «случайном блуждании»), значения можно легко восстановить, используя следующее простое правило: для узла с K ссылками (страница с K ссылками на другие страницы), вероятность каждой ссылки равна 1/K. Таким образом, матрица вероятностного перехода имеет вид

где значения 0,0 заменены на ‘.’ для удобства чтения. Перед дальнейшими вычислениями мы можем заметить, что эта цепь Маркова нередуцируема, а также апериодична и, следовательно, после длительного прогона система сходится к стационарному распределению. Как мы уже видели, мы можем вычислить это стационарное распределение, решив следующую задачу о левом собственном векторе
Таким образом, мы получаем следующие значения PageRank (значения стационарного распределения) для каждой страницы
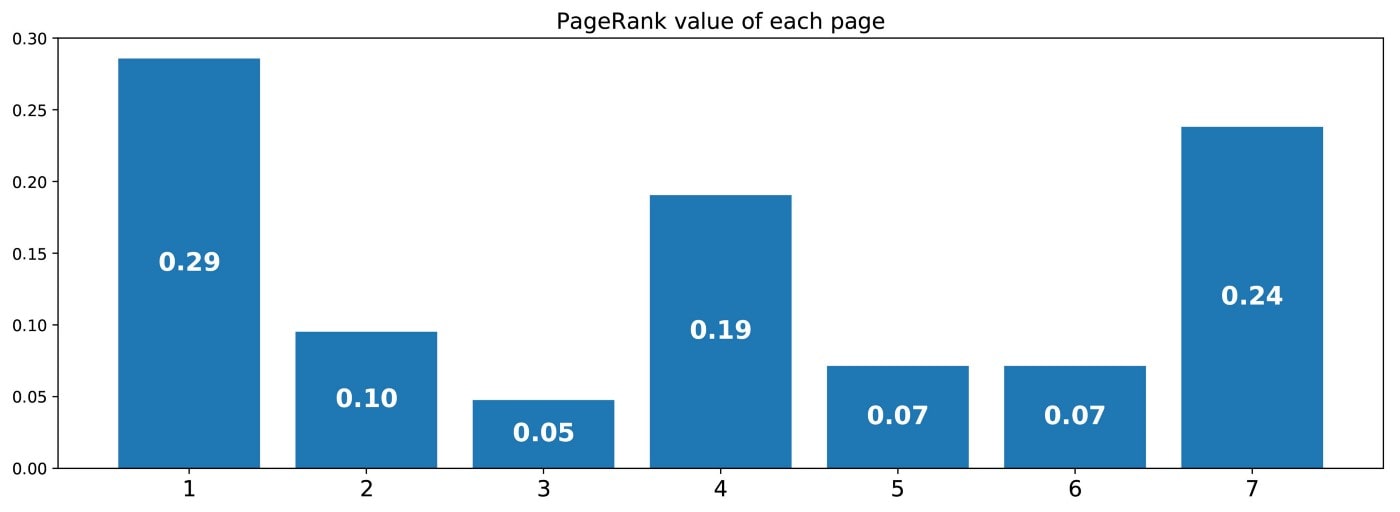
Рейтинг PageRank этого крошечного сайта будет следующим: 1 > 7 > 4 > 2 > 5 = 6 > 3.
Основные выводы
Основными выводами из этой статьи являются следующие:
- случайные процессы — это совокупности случайных величин, часто индексированных по времени (индексы часто представляют дискретное или непрерывное время)
- свойство Маркова для случайного процесса гласит, что, учитывая настоящее, вероятность будущего не зависит от прошлого (это свойство также называют «свойством отсутствия памяти»)
- цепи Маркова с дискретным временем — это случайные процессы с дискретными временными показателями, для которых выполняется свойство Маркова
свойство Маркова цепей Маркова делает исследование этих процессов гораздо более простым и позволяет вывести некоторые интересные явные результаты (среднее время повторения, стационарное распределение…) - одна из возможных интерпретаций PageRank (не единственная) состоит в том, чтобы представить себе интернет-пользователя, который случайно переходит от страницы к странице, и принять индуцированное стационарное распределение по страницам как фактор ранжирования (грубо говоря, наиболее посещаемые страницы в стационарном состоянии должны быть теми, на которые ссылаются другие очень посещаемые страницы, а затем должны быть наиболее релевантными).
В заключение еще раз подчеркнем, насколько мощными являются цепи Маркова для моделирования задач, когда приходится иметь дело со случайной динамикой. Благодаря своим хорошим свойствам, они используются в различных областях, таких как теория очередей (оптимизация работы телекоммуникационных сетей, где сообщения часто должны конкурировать за ограниченные ресурсы и становятся в очередь, когда все ресурсы уже распределены), статистика (известный метод генерации случайных величин «Markov Chain Monte Carlo» основан на цепях Маркова), биология (моделирование эволюции биологических популяций), информатика (скрытые модели Маркова являются важными инструментами в теории информации и распознавании речи) и другие.
Очевидно, что огромные возможности, которые предлагают цепи Маркова в плане моделирования, а также в плане вычислений, выходят далеко за рамки того, что было представлено в этом скромном введении, и поэтому мы призываем заинтересованного читателя прочитать больше об этих инструментах, которые полностью занимают свое место в инструментарии (data) scientist.
Спасибо за чтение!
Возможно вам будет интересно: