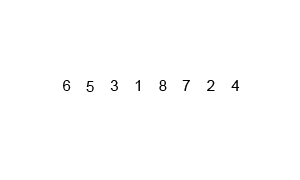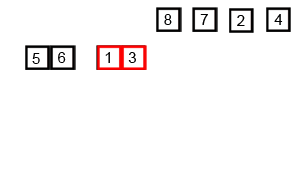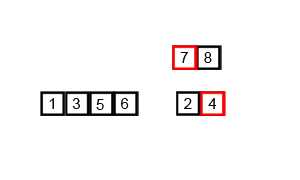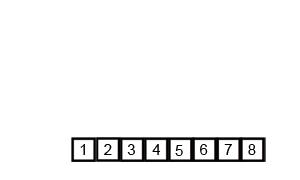Для кого написана эта статья про Алгоритмы
Если ты вообще не понимаешь ничего в программировании и хочешь с чего-то начать, но не знаешь с чего именно, то информация, которую ты здесь получишь, станет хорошим «entry point» в мир разработки.
Если ты учишься и мечтаешь стать хорошим программистом, то материал который будет освещен — именно для тебя.
Если ты уже хороший программист и хочешь стать еще и лучшим, то темы, которые будут раскрыты, тебе пригодятся.
Если ты уже senior-помидор, гуру программирования и познал «дзен», то бери свой кофе, садись поудобнее и проверь, не заржавел ли еще и помнишь ли азы.
Если ты готовишься к собеседованию в топ компанию — этот материал поможет тебе в подготовке.
Если ты хочешь зарабатывать больше — твоя прибыль вырастет, потому что работодатели ценят людей с такими знаниями.
Если ты хочешь решать действительно тяжелые и интересные задачи, где надежность и производительность являются ключевыми — написанное именно для тебя.
Данную статью можно использовать как для обучения, так и в качестве пособия, к которому возвращаешься, чтобы подсмотреть в случае, если забыл или сомневаешься, какую структуру данных выбрать или если знаешь точно, какую, но не помнишь, как именно ее эффективно применить.
Также, это хорошая практика языка программирования С++, потому что я буду использовать его в своих примерах. Кто думает, что это тяжелый язык, увидит — не такой страшный монстр, как его рисуют. Но сразу скажу: я не буду подробно останавливаться на тонкостях С++ (шпаргалка по C++). Нужно понимать, что различные подходы, алгоритмы и структуры данных не зависят от языка.
Поэтому ты можешь делать все то же самое, но использовать комфортный язык программирования вместо предложенного.
Для чего и что это вообще
Ты сейчас скажешь что-то типа: «В наши дни очень мощные машины, которые «вытянут» все, и я не должен заморачиваться с этими алгоритмами.»
Не все машины мощные, например: телевизоры, игровые консоли, медицинские устройства и так далее. Они очень ограничены и для них критически важно создавать производительные программы. Сверхмощными являются компьютеры или смартфоны, но вместе с мощным железом появляются такие же мощные запросы, которые нужно решать — большее количество пользователей, данных, новый функционал, который было невозможно реализовать раньше.
Нам бы не помогли самые новые и мощные машины, если продукты, которыми мы пользуемся, не оптимизировались самым эффективным способом. Вспомни, сколько раз после обновления какой-то программы она начинала «подтупливать», а через несколько дней после еще одного обновления все снова работает безупречно. Программисты нашли проблемное место и заменили медленный код на более эффективный. Поэтому даже самую мощную машину можно перегрузить неэффективным алгоритмом.
Приведу пример из личного опыта: внезапно в производительной системе перестал работать один очень важный функционал, который был реализован много лет назад (более 10) и который используется заказчиками компании по всему миру каждый день. До этого времени все работало, как швейцарские часы, и никто в эту часть кода с тех пор не заглядывал. Компания начала терять огромные деньги каждую минуту, а самое страшное — репутацию и клиентов. «Backup» не помог.
Конечно, это вызвало панику у руководства и меня попросили разобраться как можно быстрее и устранить проблему. После анализа я нашел проблемное место: реализация, которую много лет назад создал программист, была неэффективной; она работала правильно, но медленно. На маленьких объемах данных это было вообще незаметно. С годами данные увеличивались, логика отрабатывала все медленнее, но никто не замечал, потому что когда ты запускаешь что-то каждый день, то не видишь разницы. В конце концов, апогей наступил и логика уже была не в состоянии освоить тот объем данных — все остановилось.
Я переделал проблемную часть и после изменений все заработало снова, более того, пользователи отметили, что функционал стал намного «user friendly» (с точки зрения отклика на их действия) и они теперь могут быстрее работать.
Важно отметить: у пользователей были сверхсовременные и мощные машины — ноутбуки, планшеты, смартфоны. Со стороны компании так же — крутейшая база данных, сверхмощные серверы. Но все это никак не помогло, потому что логика обработки была неэффективна. Проблему можно было предотвратить с самого начала, 10+ лет назад, написав эффективный код, который бы одинаково быстро работал, как тогда на старых, так и сейчас на современных машинах.
Программист не мыслил алгоритмически и не думал о последствиях. Предположу, что даже не догадывался, что делает что-то не так, и не знал, есть ли вариант сделать существенно лучше.
Будем считать, разобрались для чего это, а теперь переходим к вопросу «Что это?».
Структура данных — это способ организации данных. В зависимости от того, какими данными мы хотим манипулировать и что с ними делать, — должны выбрать ту или иную структуру данных, которая идеально подходит для нашего случая.
Например, у меня есть несколько учебников, которые каждый день нужно носить с собой. Это мои данные. Также имею дома, скажем: рюкзак, чемодан для путешествий на колесиках и деревянный ящик. Это мои структуры данных. 100% не выберу деревянный ящик, потому что он тяжелый и большой. Буду тратить много усилий, к тому же стану значительно медленнее. Мне такой вариант не подходит. Далее, есть дорожный чемодан, он уже выглядит не так страшно, но все равно, ради нескольких учебников не буду каждый день ездить с ним. Это не удобно и, опять же, тратится лишнее время и силы, чтобы справиться с ним. И вот, наконец, рюкзак, который подходит идеально и решает мою проблему эффективно. С ним я становлюсь мобильный, не трачу лишнее время и силы, обе руки свободны.
Зная данные и условия — выбираю рюкзак. Но нужно помнить — это не значит, что я не могу достичь той же цели с ящиком или чемоданом. Конечно могу, вопрос лишь в том, чего это мне будет стоить.
Как же все изменится, если мои данные — не пара учебников, а, скажем, одежда для зимнего отдыха, и мне не нужно носить ее с собой каждый день. Только перевезти вещи от дома до отеля и обратно. Рюкзак не подходит, потому что маловат, и не все нужные вещи поместятся, а о ящике вообще молчу. Конечно, буду рад дорожному чемодану. А вот если мне нужно где-то в подвале хранить строительный инструмент, который очень редко достаю, то деревянный ящик пригодится. Это практично, и с ним ничего не случится через десятки лет, его невозможно испортить инструментами — чего не скажешь о рюкзаке или чемодане.
Какой вывод можно сделать из этого — не бывает ненужных структур данных, просто каждая из них подходит под конкретные цели.
Поэтому очень важно для программиста знать их все и, понимая условия задачи, выбрать правильную. Чтобы не быть похожим на того, кто каждый день носит учебники в чемодане или едет в путешествие с вещами в деревянном ящике =)
Алгоритм — это последовательность действий, которая будет выполнена для достижения цели при манипулировании входными данными. Алгоритм может отличаться в зависимости от того, какую структуру данных мы выбираем. Почти всегда есть возможность решить проблему несколькими способами, применяя различные алгоритмы. Какие-то будут эффективными, а другие — неэффективными.
Именно поэтому крайне необходимо иметь возможность оценить эффективность алгоритма по сравнению с другими, чтобы точно определить, какой лучше. Эта оценка называется — Сложность алгоритма. Об этом и пойдет речь в следующем разделе.
Сложность алгоритма и Big O
Это очень важная тема, поэтому посвящу много времени этому разделу. Многие путаются в понимании этих понятий, но я попробую объяснить просто и на примерах. В конце раздела проверим знания и потренируемся.
Сложность алгоритмов — это оценка работы алгоритма. Используется для сравнения с другими, которые приводят к одному и тому же результату. В программировании важны два ключевых фактора сравнения — время и память.
В обоих случаях сложность зависит от входных данных: список из 10 клиентов отработает быстрее и займет меньше памяти, чем аналогичный из 100 000. Причем точное время никого не интересует: это зависит от языка программирования, типа данных, процессора и многого другого. Важна только сложность при стремлении размера входных данных к бесконечности (асимптотическая сложность) — то есть, как будет расти расход ресурсов (времени и памяти) с увеличением входных данных.
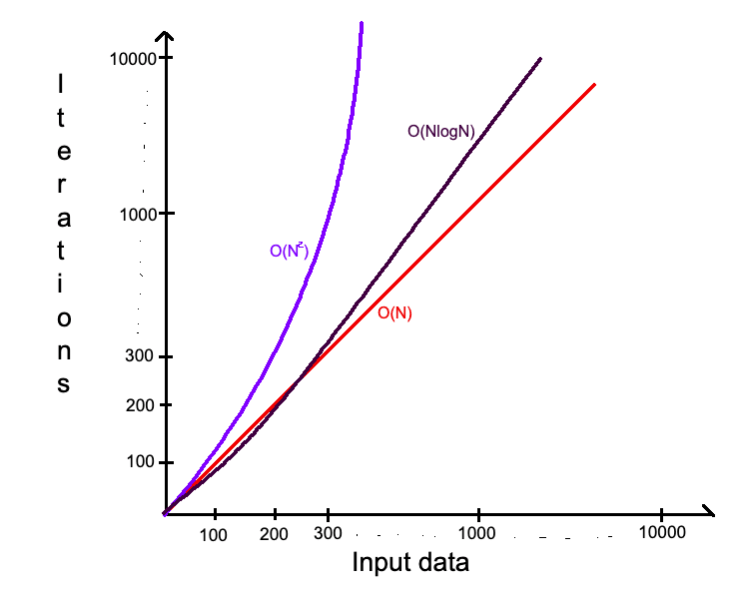
Следить за ростом и в сравнении расхода ресурсов поможет понятие «Big O» (О-нотация, как ее называют). О пришла в IT-мир из математики, но я на этом сейчас не буду останавливаться. Для нас достаточно сказать, что Big O — это описание верхнего возможного предела. Сейчас на примере объясню, что это значит.
Сначала поговорим о времени (Time Complexity, или просто TC)
Например, есть int массив, который имеет N элементов. Алгоритм печати всех значений массива будет иметь сложность алгоритма O(N), потому что нужно проверить каждый элемент массива. Количество элементов массива = количество итераций в цикле. Если 10 элементов, то 10 итераций — если 100 000, то 100 000.
void printArray(vector<int> arr)
{
for(int i = 0; i < arr.size(); ++i)
cout << arr[i] << endl;
}
В этом примере, мы точно знаем, что сложность не изменится и всегда будет O(N), потому что невозможно проверить все элементы массива сделав меньше итераций. Чего нельзя сказать о следующем примере:
Имеем тот же массив, но нам нужно печатать до тех пор, пока мы не встретим целевое значение, которое передано параметром.
void printArrayUntilGoal(vector<int> arr, int goal)
{
for(int i = 0; i < arr.size(); ++i)
{
cout << arr[i] << endl;
if(arr[i] == goal) return;
}
}
goal (целевое значение) может находиться где угодно — первый элемент массива, последний, где-то посередине, или вообще не находиться в массиве (тогда напечатаются все числа).
Но мы четко можем сказать, что сложность алгоритма не превысит O(N), хотя меньше — вполне возможно.
Вот этот максимально возможный предел и есть Big O. Это очень похоже на отношение «меньше или равно» (<=). Если у меня есть 100 гривен в кошельке, то я могу потратить меньше или ровно 100, но никак не больше.
Переходим к памяти (Space Complexity, или просто SC)
Каждый хороший программист должен заботиться об объеме затраченной памяти или пространства. Пространственная сложность является параллельным понятием временной сложности. То есть, с одной стороны существует верхний предел времени — TC, а с другой верхний предел пространства — SC. Нужно думать об обеих сложностях одновременно.
Бывают задачи/проекты, где нужно пренебречь одним показателем ради другого. Собственный пример: проект по миграции очень большого количества данных. Заказчик сразу отметил, что ему не важно, сколько времени будет отрабатывать логика. Главное, чтобы все было перенесено корректно. Как руководитель и исполнитель проекта я детально проанализировал требования и условия, и принял решение пренебречь временем ради памяти, так как потенциально память могла бы стать проблемным местом. Таким образом функционал был максимально эффективно адаптирован под SC, запускался порционально в фоновом режиме ночью.
Таких примеров может быть очень много, но возьмем за правило, что всегда нужно заботиться о TC & SC одинаково, и пытаться максимально оптимизировать, если нет никаких дополнительных обстоятельств.
Посмотрим на первый пример — O(N) TC. Что мы можем сказать о SC? Тратится ли дополнительное пространство? Нет, потому что логика «бегает» по входному массиву. Поэтому можно сказать так: данный алгоритм имеет O(1) SC. О(1) используется для описания константной сложности алгоритма.
Сейчас будет то, что очень часто вижу в реальных алгоритмах:
void printArray(vector<int> arr)
{
vector<int> a = arr;
for(int i = 0; i < a.size(); ++i)
cout << a[i] << endl;
}
Создается новый массив, такого же размера, как и входной, и копируются все данные. На результат этот «move» никак не повлияет.
Что теперь с Big O:
TC — O(N), как и раньше, потому что алгоритму нет разницы, каким именно массивом «ходить». Поскольку размер массива не изменился — количество итераций остается таким же.
SC — стало O(N), а было О(1) (не учитываю входной массив, потому что мы никак на это повлиять не можем). Создана копия входного массива и для нее выделен такой же объем памяти. То есть, мы сделали хуже, тратя дополнительный ресурс, и алгоритм теперь менее эффективен. Была ли какая-то необходимость в выделении дополнительного пространства? Нет.
Очень часто каждый программист пишет что-то подобное, не задумываясь, как это влияет на расход ресурсов. «Работает — вот и хорошо, значит, я молодец и все правильно сделал! Юхуууууу». Но важно тщательно планировать логику и проверять код после написания, по возможности, избавляясь от лишнего.
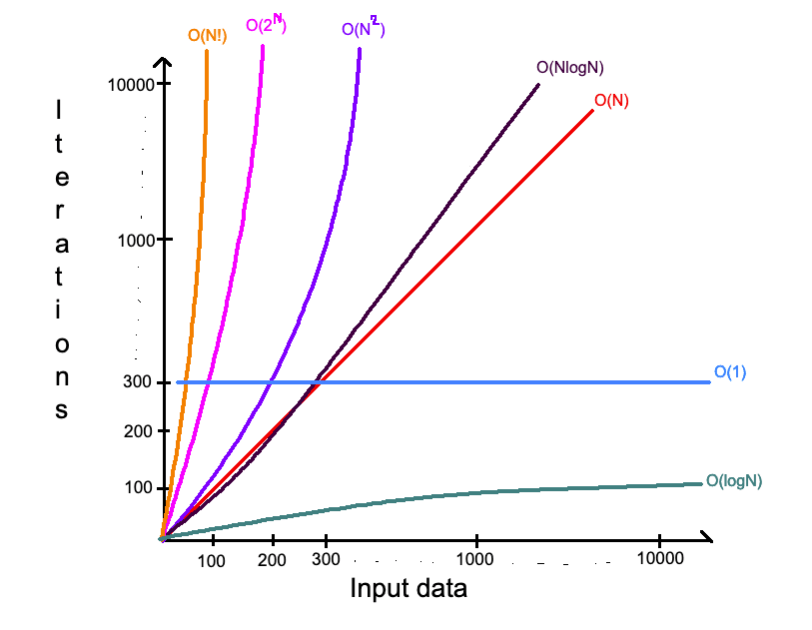
Далее поговорим о том, какие Big O бывают, какая между ними разница и как их сравнивать.
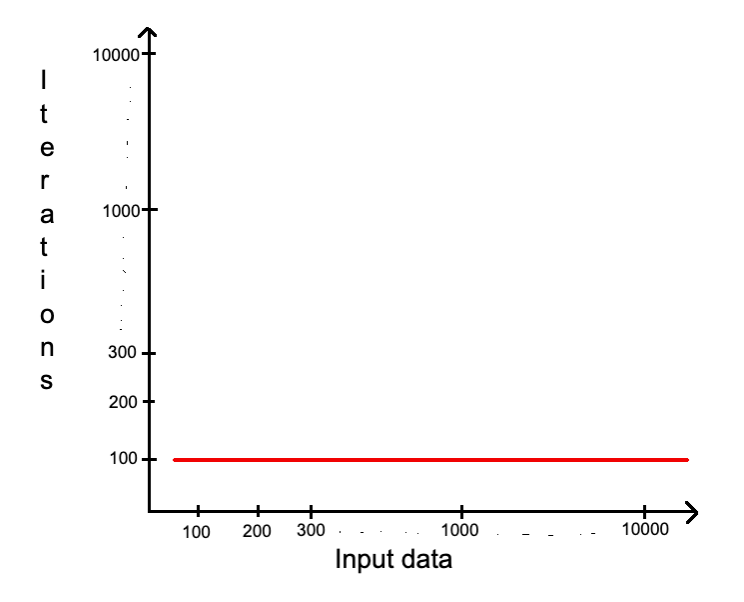
О(1) — Константная сложность (Constant)
Алгоритм имеет О(1) сложность — когда известно, сколько точно раз что-то произойдет, или сколько памяти будет выделено, независимо от изменения входных данных. То есть, алгоритм всегда будет использовать одинаковое количество ресурсов. Это наилучшая возможная сложность, к которой нужно стремиться.
Посмотрим на несколько примеров.
Пример №1:
int n = 100;
for(int i = 1; i <= n; ++i)
cout << i << endl;
Алгоритм печатает числа от 1 до 100. Сложность TC и SC — О(1), потому что мы точно знаем, сколько итераций нужно (100) и сколько памяти будет выделено. В С++ int переменная всегда занимает 4 байта, в нашем примере 2 переменные (n и і), которые требуют 4+4 = 8 байтов. Мы знаем точное количество поэтому и О(1).
Пример №2:
vector<int> a = {1,2,3,4,5};
for(int i = 0; i < a.size(); ++i)
cout << a[i] << endl;
Алгоритм печатает все элементы массива. Известно, что в массиве 5 элементов, поэтому цикл выполнится ровно 5 раз, а значит О(1) TC. Поскольку известно количество элементов и тип, то можем посчитать, сколько памяти понадобится — 5 (эл. массива) * 4 (байты за каждый) + 4 (байты за i) = 24 байта. Зная точное количество пространства, можно уверенно сказать — О(1) SC. Далее я не буду в каждом примере считать память — принцип подсчета неизменен, и у тебя есть возможность потренироваться.
Кстати, ты можешь спросить: «Жека, подожди, но ведь доступ к массиву чего-то стоит?». Мой тебе персональный «лайк», если ты задумался над таким вопросом. Отвечаю: конечно, стоит, но доступ к любому элементу массива имеет О(1) сложность, о которой ты читаешь прямо сейчас. Это возможно благодаря свойству этой структуры данных — подробнее описываю в разделе о массивах, залетай!
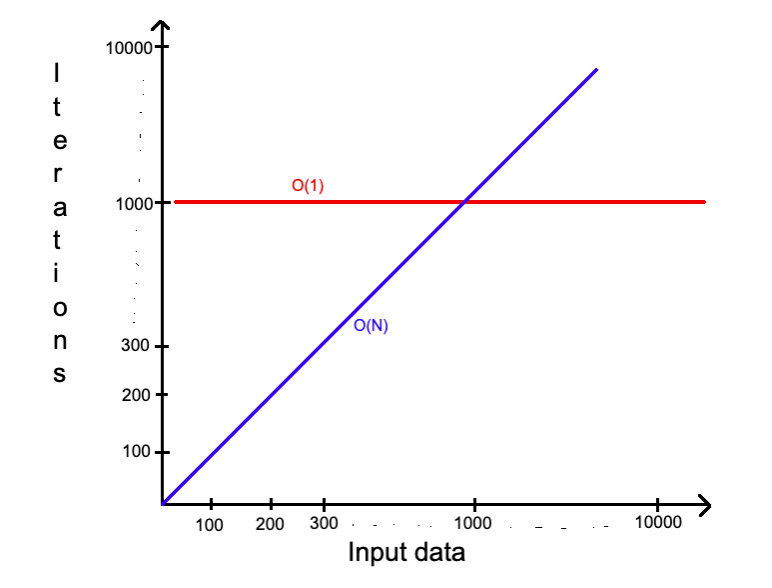
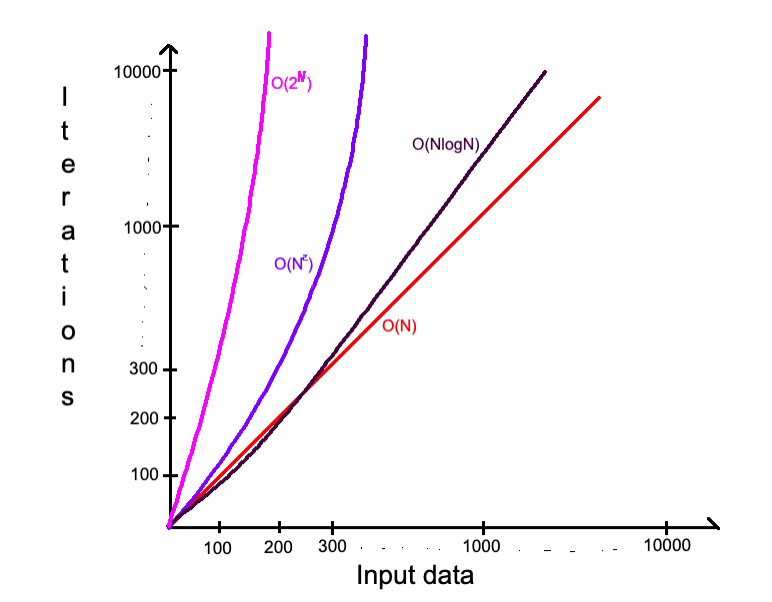
Вполне вероятно, что не константная сложность будет быстрее константной.
Например, О(N), о котором пойдет речь далее в разделе, быстрее чем О(1). Скомбинируем несколько предыдущих примеров:
void printArray(vector<int> arr)
{
vector<int> a = {1,2,3,4,5};
for(int i = 0; i < a.size(); ++i)
cout << a[i] << endl;
for(int i = 0; i < arr.size(); ++i)
cout << arr[i] << endl;
}
ʼaʼ — всегда имеет 5 элементов. ʼarrʼ может быть пустой, иметь менее 5, или намного больше. Из-за того, что не известна длина ʼarrʼ этот алгоритм не является О(1), а O(N) где N — длина ʼarrʼ. Пока известна длина, то нет разницы насколько ʼarrʼ большой (100 или 10000000 элементов) — ʼarrʼ может быть еще больше и «расти» быстрее, догнав и обогнав константу рано или поздно:
Из этого вытекает правило — константные величины отбрасываются, несмотря насколько они велики, потому что на стремление к бесконечности это существенно не повлияет.
О(N) — Линейная сложность (Linear)
В предыдущих примерах нам уже пришлось столкнуться с этой сложностью. Здесь все довольно понятно:
TC — количество итераций = количество элементов.
SC — если нужно создать массив из N элементов, то это будет O(N) SC.
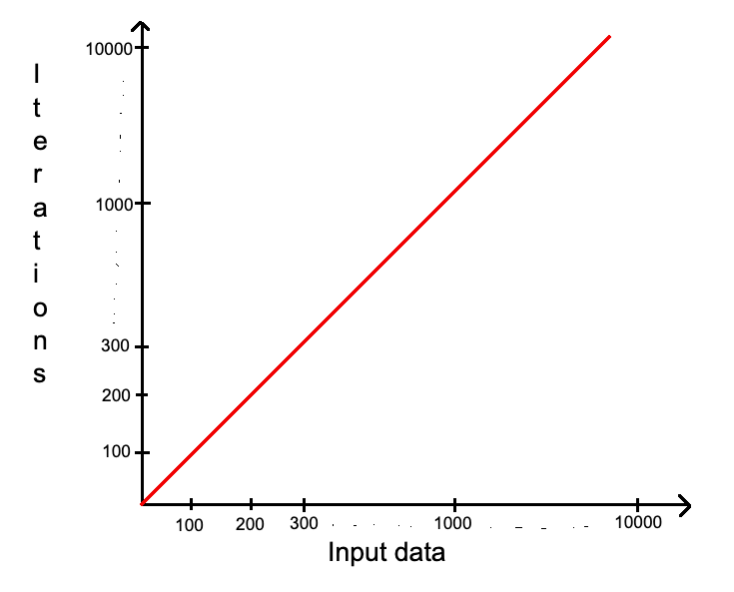
Пример:
На вход дается массив чисел. Зная заранее, что каждое число не меньше 0, и не больше 100. Требуется найти и напечатать минимальное и максимальное значение:
void findMinMax(vector<int> arr)
{
int min = 101; // Знаючи з умови, що 100 може бути максимум
int max = -1; // Знаючи, що 0 мінімум
for(int i = 0; i < arr.size(); ++i)
{
if(arr[i] < min) min = arr[i];
if(arr[i] > max) max = arr[i];
}
cout << "Min - " << min << endl;
cout << "Max - " << max << endl;
}
TC — O(N), потому что количество итераций зависит от размера ‘arr’.
SC — O(1), потому что создали только несколько переменных и известно, сколько нужно памяти.
Сравним с примером, алгоритм которого делает все то же самое, но по-другому:
void findMinMax(vector<int> arr)
{
int min = 101;
int max = -1;
for(int i : arr)
if(i < min) min = i;
for(int i : arr)
if(i > max) max = i;
cout << "Min - " << min << endl;
cout << "Max - " << max << endl;
}
TC — O(N+N) = O(2N), через 2 цикла. Но помним правило, что константу всегда отбрасываем. Поэтому сложность — O(N).
SC — O(1) без изменений.
О(log N) — Логарифмическая сложность (Logarithmic)
Почему-то это одна из самых трудных для понимания, но в то же время одна из самых важных, потому что многие алгоритмы имеют такую сложность.
Я сначала приведу очень простой пример из реальной жизни, а потом объясню, что означает магическое «log» и откуда оно берется.
Представь, что пьешь дома кофе с товарищем, и на столе лежит торт «Наполеон» длиной 16 см. Сначала режешь его пополам — съели половину. Осталось 8 см. Опять режешь пополам — съели. Осталось 4. И так продолжаешь до конца:
N = 16 — [—————-] N = 8 — [———] N = 4 — [—-] N = 2 — [—] N = 1 — [-]
Кто-то один доест 1 см торта, потому что дальше резать не получится.
Сколько раз пришлось резать торт? — 4 раза.
Возможно задать вопрос — сколько раз нужно 1 умножить на 2, чтобы получить 16 (или N в общем случае)?
N = 1
N = 2 (N*2 => 1*2)
N = 4 (N*2 => 2*2)
N = 8 (N*2 => 4*2)
N = 16 (N*2 => 8*2)
Имеем такую формулу — 2k = N, де k — количество разрезов.
Это именно то, что в математике выражает log:
og2N = k ⇔ 2k = N
В нашем случае:
log216 = 4 ⇔ 24 = 16
Когда говорят о сложности алгоритма, то основание логарифма опускают — O(log N). Основание не имеет значения для целей «Big O».
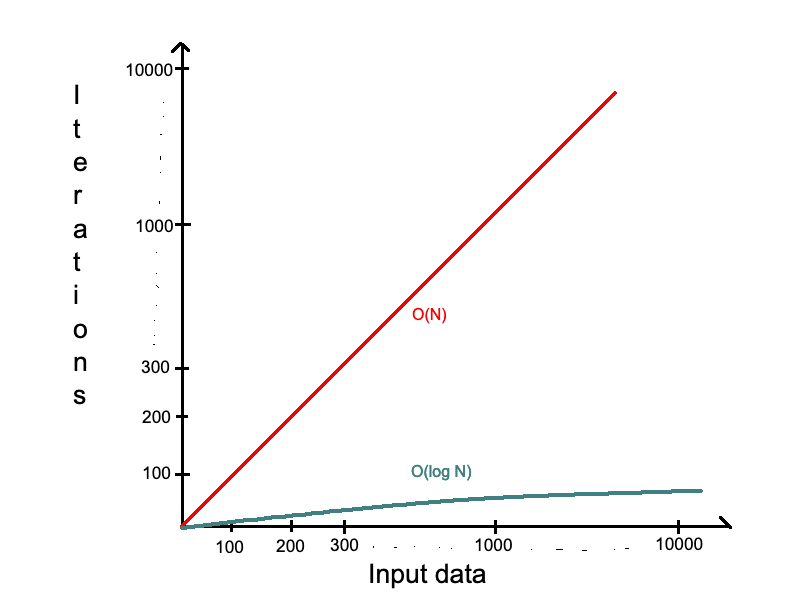
Многие алгоритмы имеют логарифмическую сложность — бинарный поиск (Binary Search), поиск в сбалансированном бинарном дереве поиска (Balanced Binary Search Tree), и многих других. Причиной этого является его эффективность, которая намного лучше чем О(N).
Пример:
Имеем 1000 элементов массива — для О(N) это 1000 итераций, а для О(log N) нужно только 9 (на самом деле 9.9657, но оставляем только целую часть).
Простой «lifehack», как понять, что алгоритм имеет O(logN) — когда на каждом шаге количество элементов уменьшается вдвое, то это скорее всего O(log N).
Многокомпонентные алгоритмы: сложение или умножение
Обычное дело, когда алгоритм имеет несколько шагов и необходимо посчитать сложность. Рассмотрим несколько примеров.
Пример № 1:
void findMinMax(vector<int> arr)
{
for(int i : arr)
cout << i << endl;
…
for(int i : arr)
cout << i << endl;
}
TC — O(N), где N длина arr. Вообще то О(N+N) = O(2N), но помним, что константу не учитываем.
Пример № 2:
void printArray(vector<int> arr)
{
for(int i : arr)
{
for(int j : arr)
{
cout << i*j << endl;
}
}
}
Или короче:
void printArray(vector<int> arr)
{
for(int i : arr)
for(int j : arr)
cout << i*j << endl;
}
Что с TC? Уже не два одиночных цикла, а один вложенный в другой. Поэтому нужно не складывать, а умножать.
ТС — О(N*N) = O(N2).
Пример № 3:
void printArray(vector<int> arr)
{
for(int i : arr)
for(int j : arr)
cout << i*j << endl;
…
for(int i : arr)
cout << i << endl;
}
В примере № 3 скомбинированы два предыдущих.
ТС — O(N2) + O(N).
Вступает в силу новое правило, которое очень похоже на предыдущее с отбрасыванием констант.
Отбрасываем все не доминирующие условия. Считаем их такими же константами. O(N2) + O(N) => O(N2) — отбрасываем O(N) потому, что не будет иметь значительной разницы в росте на фоне доминирующего O(N2).
Это правило действует только дня одного набора входных данных.
Пример № 4:
void print2Arrays(vector<int> arr1, vector<int> arr2)
{
for(int i : arr1)
cout << i << endl;
for(int i : arr2)
cout << i << endl;
}
TC — (N + M), где N — длина arr1, а M — длина arr2.
Как результат — печатаются сначала элементы arr1, а затем arr2. Если arr1 имеет 5 элементов, а arr2 имеет 10 элементов, то общее количество итераций будет 5+10 = 15.
Пример № 5:
void print2Arrays(vector<int> arr1, vector<int> arr2)
{
for(int i : arr1)
for(int j : arr2)
cout << i+j << endl;
}
TC — (N * M), где N — длина arr1, а M — длина arr2.
Как результат — каждый элемент из arr1 будет добавлен к каждому элементу arr2, и будет напечатана сумма. Если arr1 имеет 5 элементов, а arr2 имеет 10 элементов, то общее количество итераций будет 5*10 = 50.
В примерах 4 и 5 ничего не известно о длине входных массивов — это не константы. Также оба могут иметь очень разные размеры, а значит — ничего невозможно сократить или избавиться.
Простыми словами, как понять, когда сложение, а когда умножение:
Если алгоритм работает по схеме «делаю это, а потом, когда закончу, делаю следующее» — сложение итераций;
Если по схеме «делаю это для каждого раза когда делаю что-то другое» — умножаем итерации.
Проверь себя, какая будет сложность:
- O(N2 + N) — (ответ — O(N2))
- O(N2 + N2) — (ответ — O(N2))
- O(N + log N) — (ответ — O(N))
- O(17567N + N + N2) — (ответ — O(N2))
- O(N + log M) — (ответ — O(N + log M))
- O(N2 + M2) — (ответ — O(N2 + M2))
- O(44N + 52N + log N + 8M + log M) — (ответ — O(N + M))
void print2Arrays(vector<int> arr1, vector<int> arr2)
{
for(int i : arr1)
for(int j : arr1)
cout << i+j << endl;
for(int i : arr2)
for(int j : arr2)
cout << i+j << endl;
}
(ответ — O(N2 + M2))
void printArray(vector<int> arr)
{
vector<int> a = {1,2,3,4,5};
for(int i = 0; i < a.size(); ++i)
for(int j = 0; j < arr.size(); ++j)
cout << a[i]+arr[j] << endl;
}
(ответ — O(5N)=>O(N))
О(N2) — Квадратичная сложность (Quadratic)
Уже много было сказано об этой сложности. Подытожу на примере: если входной массив имеет 5 элементов, то итераций будет 25 (5*5). Это популярная сложность для некоторых алгоритмов сортировки и классическая при работе с матрицей (двумерный массив, о котором мы поговорим подробно в разделе о массивах).
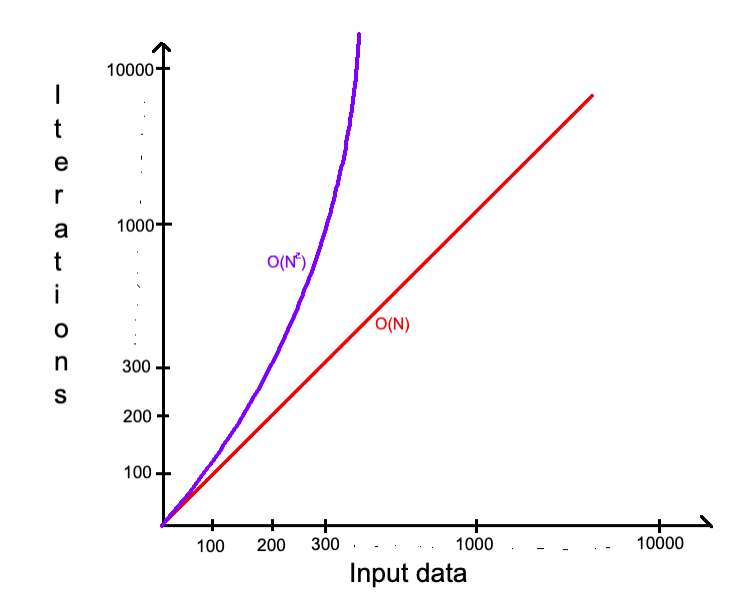
Также вполне возможны сложности — O(N3), O(N4), … , O(NN). На них я сейчас останавливаться не буду, так как они похожи, но отличаются только скоростью роста и встречаются реже.
О(NlogN) — Линейно-логарифмическая сложность (Linearithmic)
Эта сложность немного медленнее линейной, но значительно быстрее квадратичной. Применяется преимущественно в эффективных алгоритмах сортировки — слиянием (Mergesort), быстрая сортировка (Quicksort), другие. Откуда появляется logN и что это такое — читай выше в подразделе о логарифмической сложности.
Разберем на примере алгоритм сортировки массива слиянием:
Разделяем массив пополам до тех пор, пока не останется по 1 или 0 элементов в каждом.
Сливаем в один массив из двух уже отсортированных подмассивов, сравнивая элементы по очереди.
Разберемся откуда берется сложность:
Разделим
| 6 5 3 1 8 7 2 4 |
| 6 5 3 1 | 8 7 2 4 |
| 6 5 | 3 1 | 8 7 | 2 4 |
| 6 | 5 | 3 | 1 | 8 | 7 | 2 | 4 |
Сливаем
| 5 6 | 1 3 | 7 8 | 2 4 |
| 1 3 5 6 | 2 4 7 8 |
| 1 2 3 4 5 6 7 8 |
N — количество элементов (в нашем случае — 8). На каждом уровне всегда одинаковое количество элементов, для которых необходима логика слияния. Слияние требует O(N), чтобы сравнить все элементы. Посмотрим на количество уровней — их будет столько сколько раз N можно разделить на 2 (в нашем случае — 3). Это как раз и есть logN = 3. Поэтому имеем O(NlogN) TC, но SC — O(N), потому что в конце будет создан массив для слияния такой же длины, как и входной массив.
O(2N) — Экспоненциальная сложность (Exponential)
Чаще всего алгоритмы с этой сложностью встречаются в рекурсии, динамическом программировании и т. д.
Пример:
int exp(int n)
{
if (n <= 1) return 1;
return exp(n - 1) + exp(n - 1);
}
Увидев ‘exp(n — 1) + exp(n — 1)’, многие скажут — квадратичная сложность или линейная(N+N = 2N = N), но это вообще не правильное утверждение.
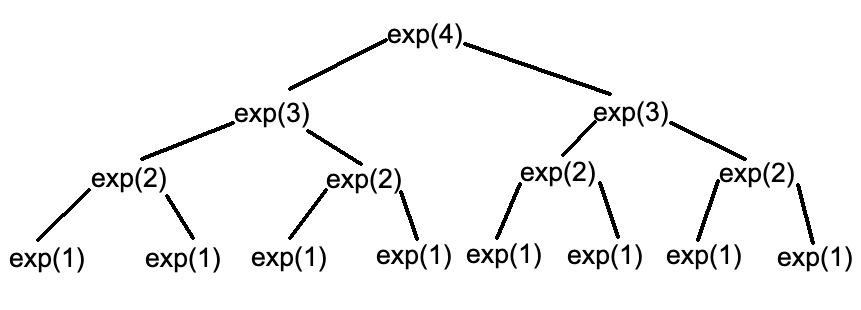
Мы можем очень просто посчитать количество вызовов самостоятельно. Пусть N = 4, тогда:
Дерево вызовов имеет глубину N. На каждом уровне вызывается функция ‘exp’ ровно 2 раза. Имеем O(2N).
Важно запомнить этот паттерн — часто (но не всегда), когда функция вызывает сама себя несколько раз, имеет сложность O (количествоВызововФункцииглыбина(количествоУровней)).
Это приводит к общему случаю — O(CN). C — любое число (количество вызовов), N — количество уровней.
Примером может быть такой алгоритм:
void exp(int n, int c)
{
if (n <= 1) return 1;
for(int i = 1; i <= c; ++i)
exp(n – 1, c);
}
O(N!) — Факториальная сложность (Factorial)
Факториал — это умножение всех целых чисел, больших 0 и не превышающих самих себя.
Например: 5! = 5*4*3*2*1 = 120.
Как можно догадаться — очень стремительно растет.
Некоторые специфические алгоритмы применяют данную сложность. Примером может быть задача с перестановкой string всеми возможными способами:
‘a’ => [‘a’] ‘ab’ => [‘ab’, ‘ba’] ‘abc’ => [‘abc’, ‘acb’, ‘bac’, ‘bca’, ‘cab’, ‘cba’]
Сейчас достаточно понимать, что алгоритмы с данной сложностью намного медленнее всех остальных (кроме O(NN)), которые обсуждались.
Также есть много других сложностей, например (O(2N*N!)), которые еще медленнее. Их все помнить не нужно, только понимать, какой быстрее. Твоя задача — всегда стараться использовать алгоритм с более быстрой сложностью, но, конечно, бывают специфические алгоритмы, требующие конкретных сложностей, даже самых медленных.
Big O — тяжелый в начале, но имея базовые знания и практикуясь на различных задачах, — понимание приходит. С опытом те же подходы будут появляться снова и снова, на «автомате» будешь выбирать, какой алгоритм применить и почему именно он подходит.
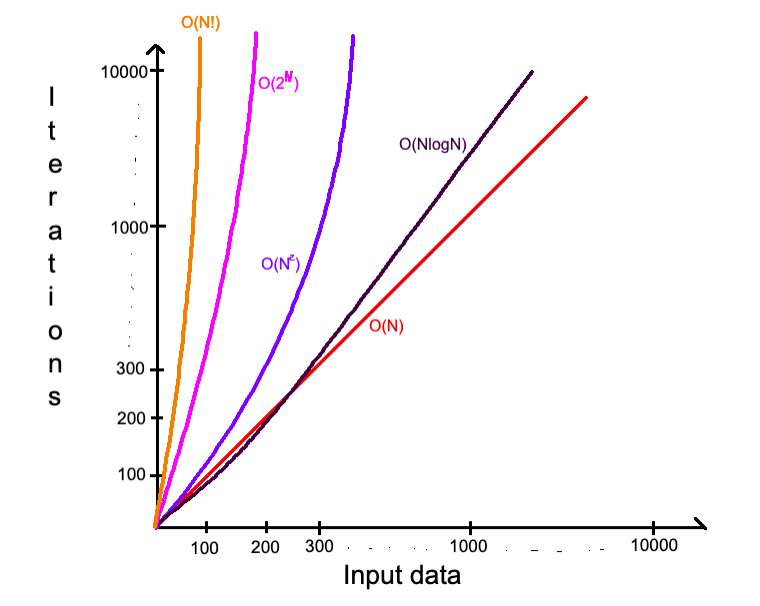
Все сложности, о которых шла речь в разделе
Примеры для оценки сложности:
1.
void print(vector<int> arr)
{
int sum = 0;
int mul = 1;
for (int i : arr)
sum += i;
for (int i : arr)
mul *= i;
cout << sum << " - " << mul << endl;
}
2.
void printPairs(vector<int> arr1, vector<int> arr2)
{
for(int i1 : arr1)
for(int i2 : arr2)
for(int j = 0; j < 999999; ++j)
cout << i1 << ',' << i2 << endl;
}
3.
void printHalf(vector<int> arr1)
{
for(int i = 0; i < arr1.size() / 2; ++i)
cout << i << endl;
}
4.
int exp(int n)
{
if (n <= 1) return 1;
return exp(n - 1) + exp(n - 1) + exp(n - 1);
}
5. Предположим, что имеем разные алгоритмы, которые решают одну и ту же задачу:
o O(2N + 589);
o O(N + C), где известно, что C меньше N в два раза;
o O(N+M);
o O(2N);
o O(N+logN);
o O(N3+10000000N);
o O(NlogN + N2);
Задача: привести сложности к норме (где возможно избавиться от констант и не доминирующих компонентов) и отсортировать от самого быстрого к самому медленному.
Структуры данных
Массив (Array)
Пожалуй, самая популярная структура данных о которой уже неоднократно упоминалось в этой статье. Пришло время разобраться.
Массив — это упорядоченный конечный набор данных (элементов) одного типа, которые хранятся в последовательно расположенных ячейках оперативной памяти. Классическим примером может быть string, который является массивом последовательных символов.
Очень важно понимать — в памяти компьютера элементы массива располагаются последовательно. Это позволяет получить доступ к любому элементу за О(1).
Пример:
int arr[5] = {1, 2, 3, 4, 5};
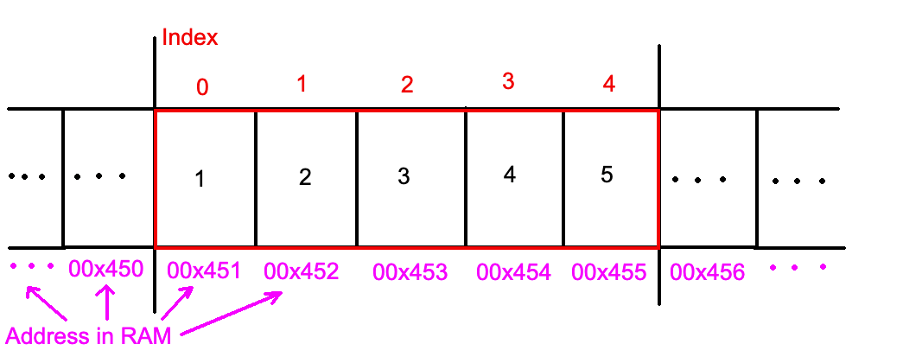
Выделено достаточно памяти для хранения всех элементов массива. В данном примере весь массив занял пространство между адресами 00×451 и 00×455 (это вымышленные для примера адреса). Причем до массива и после могут быть расположены какие-то данные, которые не относятся к этому процессу.
Когда идет обращение к массиву, то компьютер знает, где начало, а индекс указывает на сколько ячеек прыгнуть.
arr[0] = 1. Для компьютера это означает — взять значение, которое лежит по адресу 00×451 + 0 = 00×451, то есть 1.
arr[3] = 4 => 00×451 + 3 = 00×454 ( 4 )
arr[6] = ? В этом случае значение будет неопределено. Каждый раз при запуске результат будет меняться в зависимости от того, что лежит по адресу 00×451 + 6 = 00×457. Именно поэтому нужно быть внимательным с индексами.
С доступом по индексу понятно — O(1). Что будет, если нужно вставить новый или удалить какой-то элемент из массива? Если логически подумать, то для этого нужно фактически создать новый массив большего размера и перенести все значения из старого, вставляя новое в нужное место. Этот процесс занимает O(N) (Исключением будет вставка в конец динамического массива (Vector в С++), там немножко другой принцип, и это тема для другой статьи).
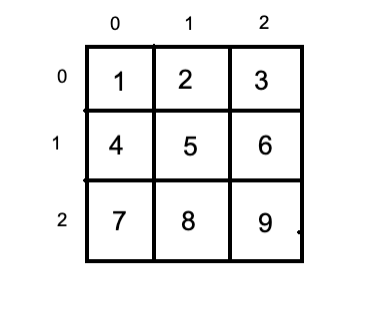
До этого мы говорили об одномерном массиве, но есть еще и двумерный (матрица):
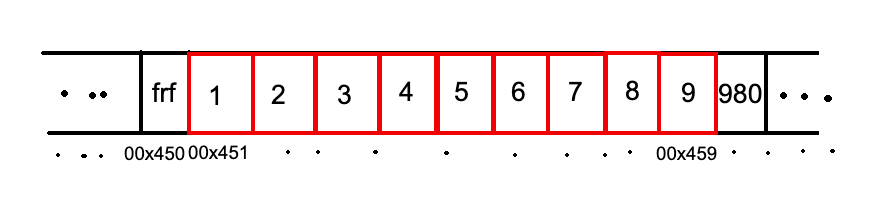
Пример:
int a[3][3] = { {1,2,3},
{4,5,6},
{7,8,9} };
a[0][2] = 3 => 00x451 + 2 = 00x453 ( 3 ).
В С++ существуют несколько способов работы с массивами:
int arr[5] = {1, 2, 3, 4, 5};
vector<int> arr = {1,2,3,4,5};
array<int, 5> arr = {1,2,3,4,5};
О преимуществах каждого можете найти записи в интернете, или пишите в комментариях, если хотите об этом отдельную статью. Лично я предпочитаю vector — удобнее для программиста, динамичнее и чаще применяется.
Связный список (Linked List)
Связный список — это структура данных, которая представляет последовательность узлов. В односвязном списке (Linked List) каждый узел указывает на следующий. Двухсвязный список (Doubly Linked List) указывает как на следующий, так и на предыдущий узлы. Первый узел называют головой (Head) списка, а последний хвостом (Tail).
Отличие от массива заключается в том, что узлы расположены в памяти хаотично, а не последовательно, как в массиве.
Linked List:
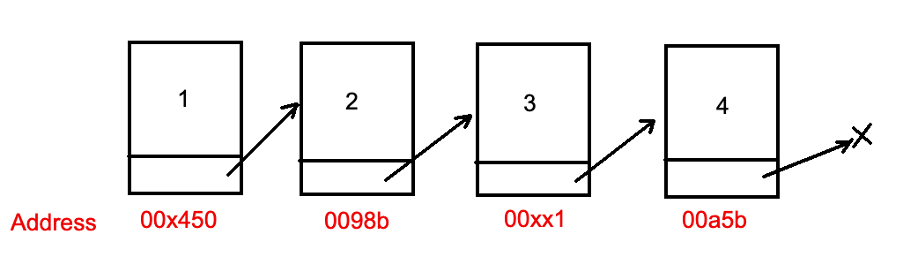
Список с двойными связями:
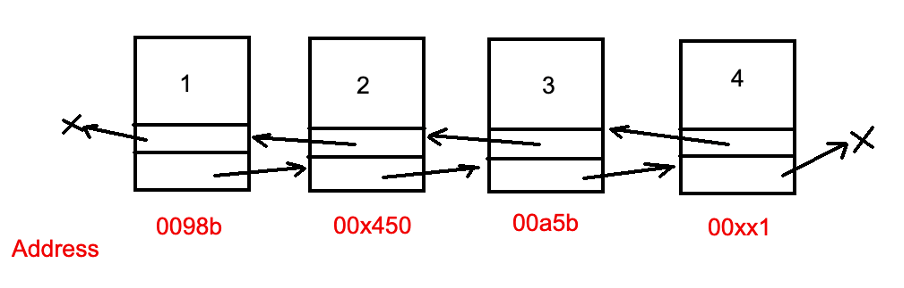
Это означает, что каждый новый узел будет создан в рандомном месте памяти, на который будет указывать другой. Получить доступ к конкретному узлу удастся, только проверяя последовательно один за другим, пока не будет найден желаемый. Поэтому, как можно понять, это будет О(N), а не О(1), как в массиве.
Но это свойство дает другое преимущество — вставлять новый узел или удалять из конца (если сохраняется Tail) или начала (Head) можно за O(1), изменив только соответствующие указатели. Также, возможно, легко вставлять или удалять узлы в середине, хотя это будет O(N), но не нужно что-то копировать.
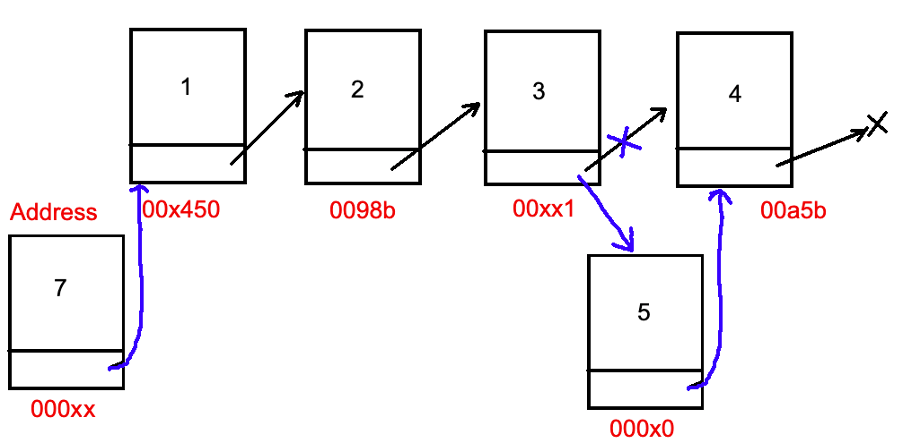
Пример:
list<int> l = {1,2,3,4};
void printList(list<int> l)
{
for(int i : l)
cout << i << endl;
}
Предыдущий пример применяет стандартный список C++, но можно легко создать свой собственный.
Пример:
Для этого нужно объявить структуру с желаемыми данными и указатель на такую же структуру:
struct Node {
public:
int data;
Node* next;
};
Затем создать саму реализацию:
int main() {
Node* head = new Node();
Node* next = new Node();
Node* tail = new Node();
head->data = 1;
head->next = next;
next->data = 2;
next->next = tail;
tail->data = 3;
tail->next = nullptr;
while (head != nullptr)
{
cout << head->data << endl;
head = head->next;
}
delete head;
delete next;
delete tail;
return 0;
}
Использование стандартного list намного удобнее, но нужно понимать, как оно работает, поэтому есть смысл потренироваться на задачах с созданием своего собственного списка.
Стек (Stack)
В моем детстве были специальные «штуки» для хранения дисков:

Если положить туда 5 дисков, то потом, чтобы достать первый положенный нужно сначала достать все остальные, но последний лежит с самого верха и его легко взять.
Так же работает и структура данных стек в программировании. Принцип работы называется LIFO (Last-In-First-Out), то есть последний пришел — первый вышел.
Нет смысла использовать эту структуру данных для доступа к какому-то элементу внутри, потому что это будет O(N). Ее ценят за 0(1), когда нужно: добавить новый элемент, прочитать последний, удалить последний, проверить, не пустой ли стек.
Классические функции:
- push(something) — добавить новый элемент;
- top() — прочитать последний элемент;
- empty() — проверить пустой стек или нет;
- pop() — удалить последний элемент.
Пример:
void workWithStack ()
{
stack<int> st;
st.push(1);
st.push(2);
st.push(3);
cout << st.top() << endl;
st.pop();
cout << st.top() << endl;
cout << "1(true) - empty, 0(false) - not empty => " <<st.empty() << endl;
while(!st.empty())
{
cout << st.top() << endl;
st.pop();
}
}
Результат:
3 2 1(true) - empty, 0(false) - not empty => 0 2 1
Очередь (Queue)
Структура данных в программировании копирует очередь в реальной жизни. Например, придя в банк, ты видишь перед собой 3 человека. Чтобы сделать то, ради чего пришел, нужно дождаться, когда закончат свои дела все предыдущие клиенты банка. Очевидно, что тот, кто был первый в очереди, первым же и закончит свои дела и пойдет домой.
Структура данных работает по принципу — FIFO (First-In-First-Out), то есть первый пришел так же первый и вышел. Имеет смысл использовать, когда нужно: читать первый элемент, удалять первый элемент, добавлять новый элемент в конец, проверять, не пустая ли очередь. Эти манипуляции будут иметь О(1).
Так выглядит очередь:
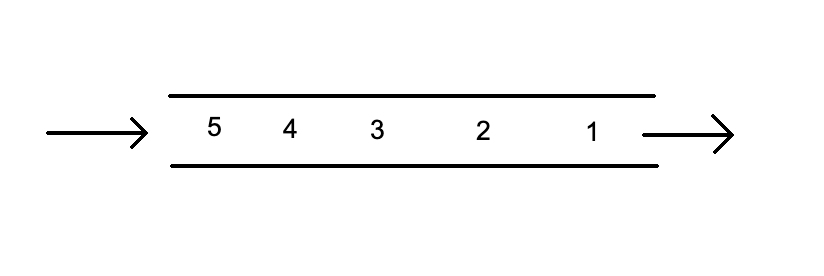
Классические функции:
- push() — добавить новый элемент в конец очереди;
- pop() — удалить элемент из начала очереди;
- front() — прочитать элемент из начала очереди;
- empty() — проверить, пустая очередь или нет.
Пример:
void workWithQueue ()
{
queue<int> q;
q.push(1);
q.push(2);
q.push(3);
q.push(4);
q.push(5);
cout << q.front() << endl;
q.pop();
cout << q.front() << endl;
cout << "1(true) - empty, 0(false) - not empty => " << q.empty() << endl;
while(!q.empty())
{
cout << q.front() << endl;
q.pop();
}
}
Результат:
1 2 1(true) - empty, 0(false) - not empty => 0 2 3 4 5
Дерево (Tree)
Дерево — это структура данных, которая состоит из узлов и связывающих их ребер. Каждое дерево начинается с корневого узла (root node), который имеет дочерние узлы (child nodes). В свою очередь, дочерние узлы могут иметь свои дочерние узлы и так далее.
Узел считается родительским (parent node) для всех своих дочерних. Таким образом корневой узел также является родительским для всех узлов дерева. Листовой узел (leaf node) — тот, у которого нет дочерних узлов. Высота дерева (height) — максимальное количество путей/ребер (edges) от корневого до листового узла (считаем ребра, а не узлы). Глубина дерева — количество ребер от узла до корневого узла.
Пример: Дерево с 10 узлами.
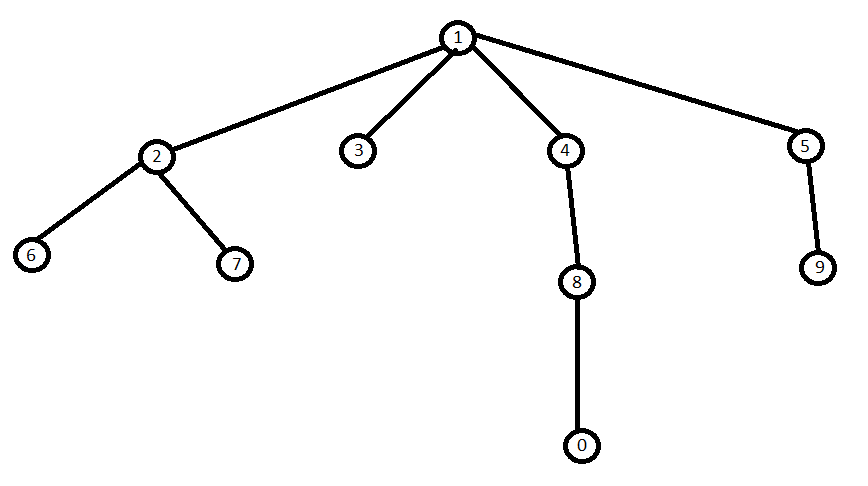
- Узел 1 — root для дерева и parent для всех остальных;
- Узел 2 — child для 1, parent для 6 и 7;
- Узлы 6, 7, 0 и 9 — leaf nodes;
- Высота дерева — 3 (1->4->8->0);
- Глубина узла 1 = 0, глубина узла 6 = 2(6->2->1), глубина узла 4 = 1(4->1).
Деревья бывают разных типов, и в зависимости от типа будет меняться алгоритм и его сложность.
Рассмотрим следующие типы:
Бинарное дерево (Binary Tree) — это дерево, в котором каждый узел имеет не более двух дочерних. На примере выше — не бинарное дерево, но ниже показано бинарное:
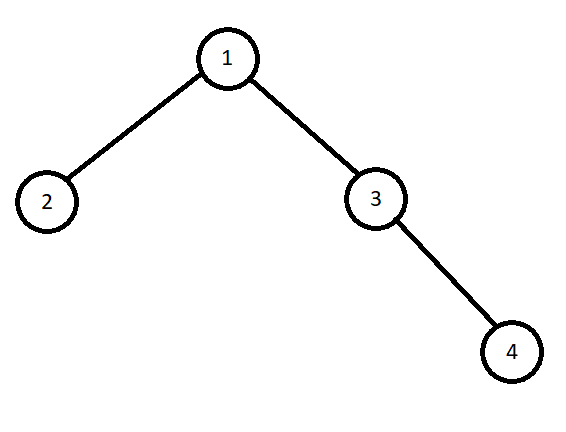
Бинарное дерево поиска (Binary Search Tree или BST) — это бинарное дерево, в котором значение левого дочернего узла меньше или равно (<=) значению родительского, а значение правого дочернего узла больше (>) (<= N(значение) <). Это свойство должен удовлетворять каждый узел дерева. (В зависимости от условий свойство может измениться. Например, если известно, что значения не будут повторяться, то свойство будет: < N <. В других случаях может быть: < N <=)
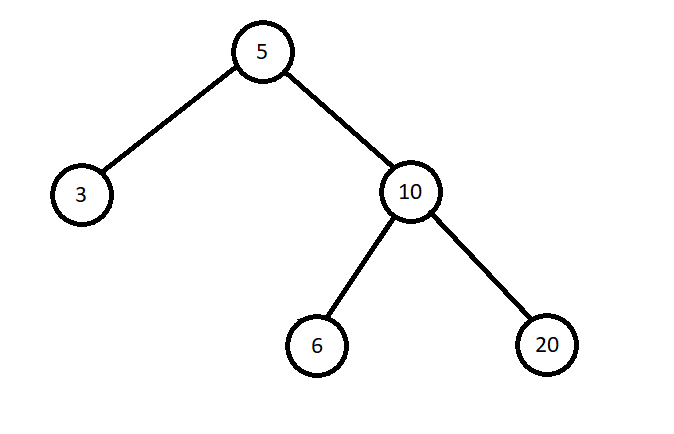
Рассмотрим на примере:

Это бинарное дерево, но не BST. Причиной этому является отмеченный красным цветом узел со значением 4. Для узла 10 свойство выполняется: 4 <= 10 < 20. Но для узла 5 — нет. 4 должно быть дочерним узлом где-то слева от 5, чтобы дерево считалось BST.
Если заменить 4, скажем, на 6, то свойство выполнится для 10 и 5 и дерево будет BST:
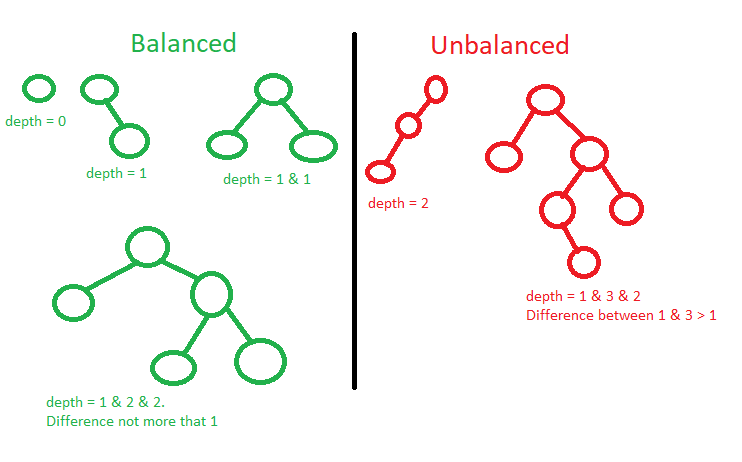
Сбалансированное и несбалансированное (Balanced/Unbalanced) — сбалансированным является дерево, у которого глубина всех листовых узлов отличается не более чем на 1. Если дерево имеет только один дочерний узел, то глубина от листового не должна быть больше 1.
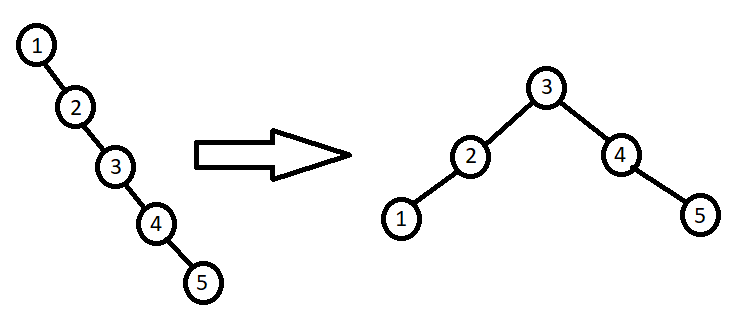
Дерево может быть BST, но не сбалансированным. Тогда, например, алгоритм вставки или поиска будет иметь сложность O(N), но если сбалансировать то же дерево — станет O(logN), потому что на каждом шаге логика будет выбирать, в какую сторону пойти, тем самым делить пополам.
Законченное бинарное дерево (Complete Binary Tree) — это дерево, в котором все его уровни полностью заполнены, за исключением, возможно, последнего. На последнем уровне дерево должно быть заполнено слева направо.
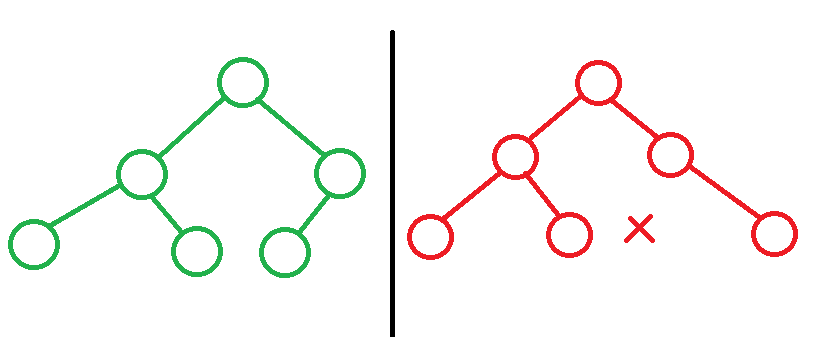
Полное бинарное дерево (Full Binary Tree) — это дерево, у которого каждый узел имеет ноль или два дочерних узла.
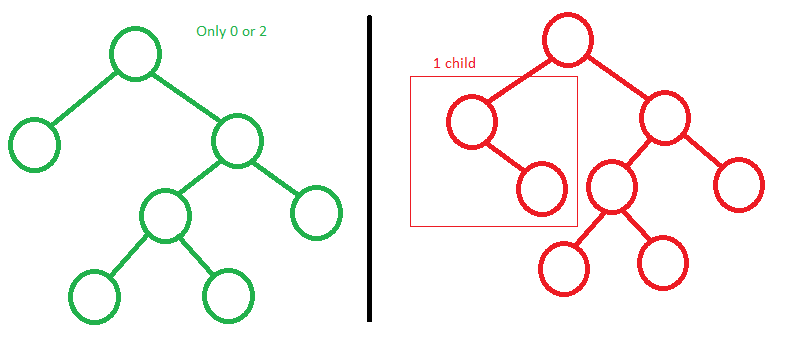
Идеальное бинарное дерево (Perfect Binary Tree) — это дерево, которое является законченным и полным одновременно. То есть все листовые узлы находятся на одном уровне, уровень в свою очередь заполнен максимально возможным количеством узлов.
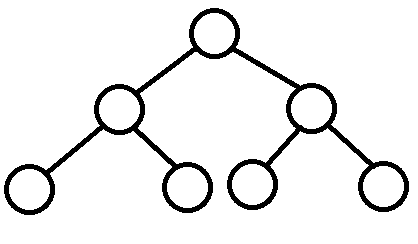
При работе с деревьями очень часто применяют рекурсию. Вообще существует много алгоритмов для работы с деревьями. Конечно, все охватить в этой статье не удастся, но я хочу рассмотреть один очень важный и простой для понимания — обход бинарного дерева (Binary Tree Traversal):
- In-Order Traversal — дойти до крайнего левого узла, сделать какое-то действие с данными, пойти вправо;
- Pre-Order Traversal — сделать какое-то действие с данными, пойти влево, затем пойти вправо;
- Post-Order Traversal — дойти до крайнего левого узла, пойти вправо, сделать какое-то действие с данными.
Пример:
Создаем бинарное дерево, заполняем данными и печатаем значения всеми способами.
struct Node
{
int data;
Node* left;
Node* right;
};
void printInorder(Node* node)
{
if(node == nullptr) return;
printInorder(node->left);
cout << node->data << endl;
printInorder(node->right);
}
void printPreorder(Node* node)
{
if(node == nullptr) return;
cout << node->data << endl;
printPreorder(node->left);
printPreorder(node->right);
}
void printPostorder(Node* node)
{
if(node == nullptr) return;
printPostorder(node->left);
printPostorder(node->right);
cout << node->data << endl;
}
int main()
{
Node* root = new Node();
root->data = 1;
root->left = new Node();
root->left->data = 2;
root->left->left = nullptr;
root->left->right = nullptr;
root->right = new Node();
root->right->data = 3;
root->right->left = nullptr;
root->right->right = nullptr;
/* 1
2 3
*/
cout << "In-order: " << endl;
printInorder(root);
cout << "Pre-order: " << endl;
printPreorder(root);
cout << "Post-order: " << endl;
printPostorder(root);
return 0;
}
Результат:
In-order: 2 1 3 Pre-order: 1 2 3 Post-order: 2 3 1
Хеш-таблица (Hash Table)
Хеш-таблица — это структура данных, которая сопоставляет ключи со значениями для высокоэффективного поиска. Помогает в решении очень большого количества задач.
Существует несколько способов реализации:
1. Массив связных списков и функция хеширования. Функция хеширования с помощью специального алгоритма генерирует для ключа значение int, которое применяется как индекс массива.
В каждой ячейке массива хранится связный список с ключом и значением. Почему именно связный список? Потому что для разных ключей функция хеширования может вернуть одинаковый индекс, по которому нужно хранить несколько значений.
Например:
Есть книга с именами и номерами телефонов.
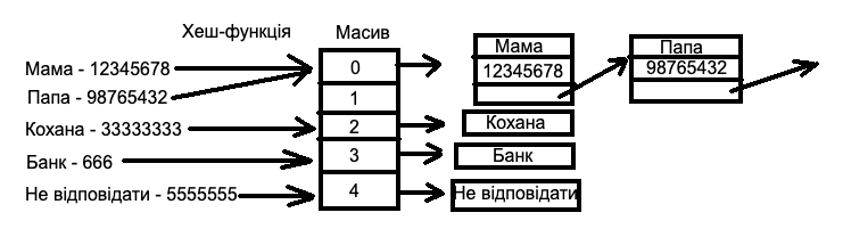
Как видим из примера — для Мамы и Папы хеш-функция вернула один и тот же индекс, по которому хранятся/ читаются данные в виде списка. Это называется коллизия (Collision). Если список имеет N имен, то коллизий, в теории, может быть столько же.
Это говорит о плохом алгоритме функции хеширования. То есть в худшем случае сложность будет O(N), потому что надо проверить каждый элемент списка, но такой сценарий очень маловероятен и обычно хеш-функция реализована хорошо, что дает O(1) TC как для добавления нового элемента в хеш-таблицу, так и для чтения.
Без хеш-таблицы, для поиска нужно было бы потратить гарантированно O(N).
В С++ такая хеш-таблица записывается:
unordered_map<key_type,value_type> name;
Пример:
Посчитать количество элементов массива и напечатать.
void countElements(vector<int> arr)
{
unordered_map<int, int> um;
for(int i : arr)
um[i]++;
for(auto pair : um)
cout << pair.first << " -> " << pair.second << endl;
}
Пусть имеем массив {3, 5, 5, 3, 7, 3, 1, 7}.
Результат:
1 -> 1 7 -> 2 5 -> 2 3 -> 3
2. Сбалансированное дерево бинарного поиска. Для построения хеш-таблицы применяется дерево.
На примере той же книжки с контактами:
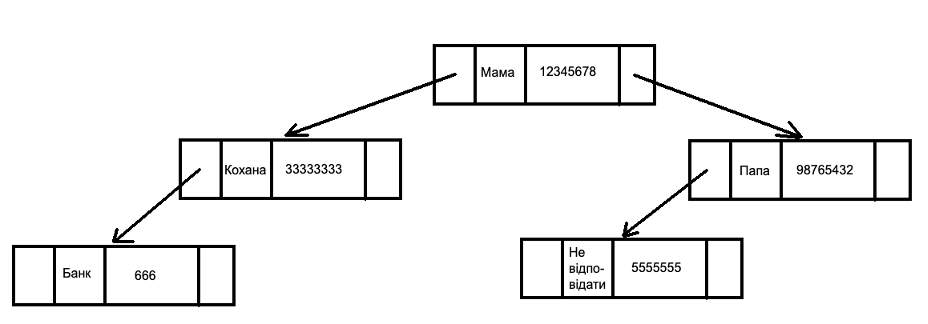
Преимуществом в применении именно этой хеш-таблицы является стабильность и отсортированный список по ключу. Сложность всегда — O(logN).
В С++ такая хеш-таблица записывается:
map<key_type,value_type> name;
Пример:
Посчитать количество элементов массива и напечатать.
void countElements(vector<int> arr)
{
map<int, int> um;
for(int i : arr)
um[i]++;
for(auto pair : um)
cout << pair.first << " -> " << pair.second << endl;
}
Стоит отметить, что map сохраняет список, отсортированный по ключу (пользуясь из дерева), а unordered_map — нет. Если нужно хранить только уникальные значения, то для этого в С++ есть: unordered_set<value_type> name и set<value_type> name. Сложность и принцип применения такой же как и у map.
Помни:
unordered_map/unordered_set имеет О(1) TC (в худшем случае O(N), что маловероятно);
map/set — имеет всегда O(logN) TC.
Граф (Graph)
Ты даже не догадываешься насколько это важная структура данных. Используется во многих алгоритмах, способных решать сложные задачи. Как пример — Google Maps, которым мы пользуемся почти ежедневно, применяет сразу два алгоритма, в основе которых лежат графы — алгоритм Дейкстры (Dijkstra’s algorithm) и алгоритм А* (эти алгоритмы не будут описаны в статье — пиши в комментариях, если хочешь о них отдельную статью).
Благодаря им можно найти кратчайший путь от точки А до точки Б. Когда ты выбираешь, как долететь, например, из Киева в Майами кратчайшим путем — алгоритм поиска на сайте подсчитает вообще все варианты и отсортирует их от самых коротких до самых длинных.
В основе лежат также графы и алгоритмы работы с ними. Примерами я хотел лишь подчеркнуть важность графов в программировании. Их еще можно приводить очень много — перейдем к определению.
Граф — это коллекция узлов (nodes) и ребер (edges). Узлы связаны с ребрами. Да, так, как и в дереве. Дерево является подвидом графа, то есть каждое дерево — это граф, но не каждый граф — дерево. Графы бывают двух типов — ориентированный/ направленный (Directed graph) и неориентированный/ без направления (Undirected graph).
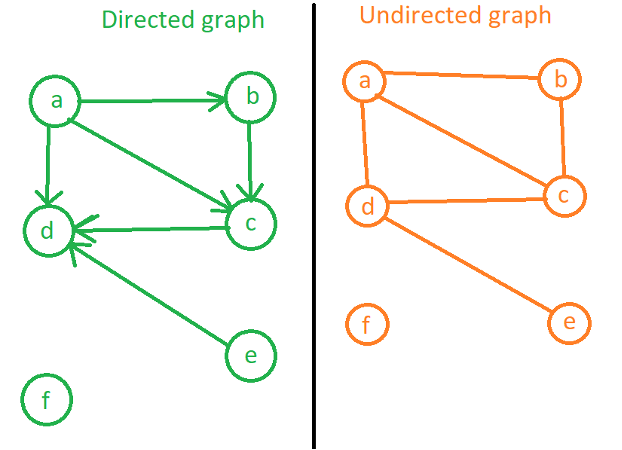
«a,b,c,d,e,f» — данные для примера, но они могут быть заменены на адреса, названия городов или аэропортов и тому подобное. Основное отличие между типами графов — направление откуда и куда можно добраться.
Например:
Куда можно попасть из «a»?
Directed: b(a->b), c(a->c, a->b->c), d(a->d, a->c->d, a->b->c->d, a->b->c->d)
Undirected: все то же самое, но добавляется — e(a->d->e, a->c->d->e, a->b->c->d->e)
Возможно ли попали из «c» в «a»?
Directed: нет, потому что из «c» только в «d». Хотя из «a» в «c» возможно.
Undirected: да, из «c» в «a» и наоборот.
Куда возможно попасть из «e»? (Напиши ответ сам для обоих типов).
Я хотел бы обратить внимание на узел «f» — также часть графа, но в обоих случаях никак не возможно попасть туда или оттуда.
Сосед — узел, который находится рядом и до которого можно добраться. Соседи «a» — «b», «c» и «d». «d» и «f» — не имеют соседей. Сосед «e» — «d».
Граф можно изобразить в виде списка совместимости (Adjacency list):
Directed:
{
a: [b,c,d],
b: [c],
c: [d],
d: [],
e: [d],
f: []
}
Undirected:
{
a: [b,c,d],
b: [a,c],
c: [a,b,d],
d: [],
e: [d],
f: []
}
Имея такой список, возможно нарисовать граф для лучшей визуализации (что было сделано в начале).
Каким образом показать такой список в С++? Очень просто — хеш-таблица, у которой ключами будут данные узла («a,b,c,d,e,f»), а значением — массив связанных с ключом узлов. Надеюсь, ты уже выше ознакомился с массивом и хеш-таблицей, если нет, то сначала ознакомься.
Для нашего примера выглядеть это будет так:
unordered_map<string, vector<string>> graph;
Важно уметь правильно построить граф и обходить его. В своем примере ниже я покажу, как это сделать, но сначала отмечу, что существует два алгоритма обхода графа (Graph traversal) — в глубину (Depth first traversal) и в ширину (Breadth first traversal).
Depth first traversal — от начального узла проверяется рандомный сосед (обычно по очереди из списка совместимости), далее от соседа к его соседу и так далее. Таким образом логика ползет в глубину. Реализовать данный алгоритм помогает стек (Stack) или же применение рекурсии. Мы рассмотрим только вариант со стеком.
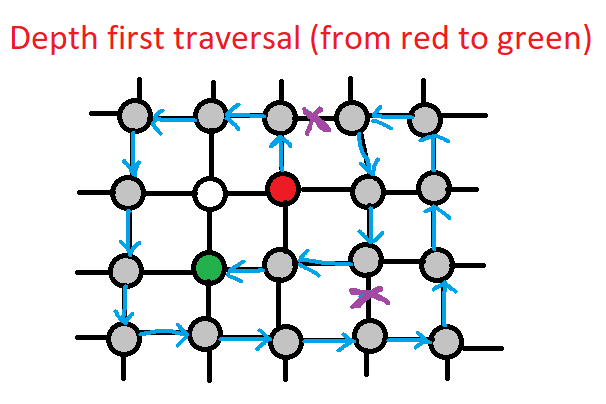
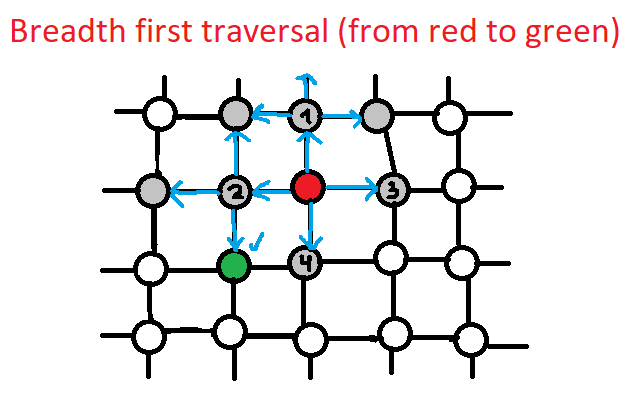
Breadth first traversal — от начального узла проверяются все соседи по очереди, затем для каждого соседа его соседи и так далее. Таким образом логика ползет в ширину. Реализовать данный алгоритм помогает только очередь (Queue).
Хотя сложность будет одинаковой для обоих(О(N+E), где N — количество узлов, а Е — количество ребер), но, как видно на рисунках, Breadth first traversal может быстрее найти нужный узел когда известно, что он ближе от стартового узла, а Depth first traversal — когда дальше.
Разберем оба алгоритма на примере печати графа (Directed).
Depth first traversal:
1. Добавляем «a» (первый из списка) в стек и запускаем внутренний цикл, пока стек не станет пустым:
1. Достаем последний из стека и печатаем — «a». Добавляем в стек соседей «a» = {«b», «c», «d»};
2. Достаем последний из стека и печатаем — «ad». Добавляем в стек соседей «d» (их нет) = {«b», «c»};
3. Достаем последний из стека и печатаем — «adс». Добавляем в стек соседей «с» («d» — уже отработанный и не
добавляется) = {«b»};
4. Достаем последний из стека и печатаем — «adсb». Добавляем в стек соседей «b» («с» — уже отработанный и не добавляется). Стек = {}. Выходим.
2. «b» — уже отработанный;
3. «c» — уже отработанный
4. «d» — уже отработанный;
5. «e» — добавляем в стек:
1. Достаем последний из стека и печатаем — «аԁсЬе». Добавляем в стек соседей «е» («d» уже был отработан, поэтому
не добавляется ) = {} — пустой поэтому выходим.
6. «f» — добавляем в стек:
1. Достаем последний из стека и печатаем — «adсbеf». Добавляем в стек соседей «f» (их нет) = {} — пустой поэтому выходим.
Результат, который напечатается: «adсbеf».
Breadth first traversal:
1. Добавляем «a» (первый из списка) в очередь и запускаем внутренний цикл, пока очередь не станет пустой:
- Достаем первый из очереди и печатаем — «a». Добавляем в очередь соседей «a» = {«b», «c», «d»};
- Достаем первый из очереди и печатаем — «ab». Добавляем в очередь соседей «b» = {«c», «d», «c»};
- Достаем первый из очереди и печатаем — «abс». Добавляем в очередь соседей «с» = {«d», «c», «d»};
- Достаем первый из очереди и печатаем — «abсd». Добавляем в очередь соседей «d» (их нет) = {«c», «d»};
- Достаем первый из очереди и печатаем («c» уже отработан, поэтому не печатаем ) — «abсd». Очередь = {«d»};
- Достаем первый из очереди и печатаем («d» уже отработанный поэтому не печатаем ) — «abсd». Очередь = {}. Выходим.
2. «b» — уже отработанный;
3. «c» — уже отработанный;
4. «d» — уже отработанный;
5. «e» — добавляем в очередь:
1. Достаем первый из очереди и печатаем — «abсdе». Добавляем в очередь соседей «е» («d» уже был отработан, поэтому не добавляем ) = {} — пустой поэтому выходим.
6. «f» — добавляем в очередь:
1. Достаем первый из очереди и печатаем — «abсdеf». Добавляем в очередь соседей «f» (их нет) = {} — пустой поэтому выходим.
Результат, который напечатается: «abсdеf».
Но надо помнить, что unordered_map не сортирует ключи — это дает О(1) TC. Если применить map, то ключи будут отсортированы, но TC — О(logN).
Как ты заметил — нужно где-то хранить узлы, которые уже были отработаны, чтобы не ходить по кругу. Для этого создаем дополнительную хеш-таблицу/набор(set):
unordered_set<string> visited;
Как ты уже знаешь, проверка есть ли элемент в set занимает O(1).
Перейдем к программированию: имеем массив пар — указывает какие узлы связаны с какими.
Задача: создать список совместимости (граф) на основе входного массива и напечатать его, применяя оба алгоритма обхода.
unordered_map<string, vector<string>> getGraph(vector<tuple<string, string>>& edges)
{
unordered_map<string, vector<string>> graph;
for(auto edge : edges)
graph[get<0>(edge)].push_back(get<1>(edge));
return graph;
}
void printDepth(unordered_map<string, vector<string>> graph)
{
unordered_set<string> visited;
stack<string> st;
for (auto pair : graph)
{
st.push(pair.first);
while (!st.empty())
{
string current = st.top();
st.pop();
if(visited.find(current) != visited.end()) continue;
visited.insert(current);
cout << current << endl;
if(graph.find(current) == graph.end()) continue;
for(int i = 0; i < graph[current].size(); ++i)
{
if(graph[current][i] != "")
st.push(graph[current][i]);
}
}
}
}
void printBreadth(unordered_map<string, vector<string>> graph)
{
unordered_set<string> visited;
queue<string> q;
for (auto pair : graph)
{
q.push(pair.first);
while (!q.empty())
{
string current = q.front();
q.pop();
if(visited.find(current) != visited.end()) continue;
visited.insert(current);
cout << current << endl;
if(graph.find(current) == graph.end()) continue;
for(int i = 0; i < graph[current].size(); ++i)
{
if(graph[current][i] != "")
q.push(graph[current][i]);
}
}
}
}
int main()
{
vector<tuple<string, string>> edges
{
{"a", "b"},
{"a", "c"},
{"a", "d"},
{"c", "d"},
{"e", "d"},
{"d", ""},
{"f", ""}
};
unordered_map<string, vector<string>> graph = getGraph(edges);
cout << "Depth:" << endl;
printDepth(graph);
cout << "Breadth:" << endl;
printBreadth(graph);
return 0;
}
Результат (у тебя может отличаться, смотря как данные хранятся в хеш-таблице):
Depth: d e f a c b Breadth: d e f a b c
Вывод и что дальше
Надеюсь, что теперь ты можешь применять знания в реальной жизни и объяснить:
- почему алгоритмы и структуры данных так важны;
- что такое сложность алгоритма и Big O;
- можешь самостоятельно посчитать сложность алгоритма;
- ориентируешься в структурах данных и имеешь понимание, в какой ситуации лучше
- применить ту или иную;
- немного подкачал свои навыки С++.
Перевод статьи Евгения Радченко