Понимаем каррирование в JavaScript
Перевод статьи Understanding Currying in JavaScript
Функциональное программирование это стиль написания кода, в котором функции передают как аргументы (колбэки) и отдают тоже функции без сайд-эффектов(изменения состояния приложения).
Множество языков приняли такую стилистику в работе с кодом. Самые популярные из них это: JavaScript, Haskell, Clojure, Erlang и Scala.
Возможностью передавать и возвращать функции породила много других концепций:
Чистые функции
Каррирование
Функции высшего порядка
И сейчас мы разберем одну из них. А именно каррирование, ну или карринг. Кому как удобно.
Что такое каррирование?
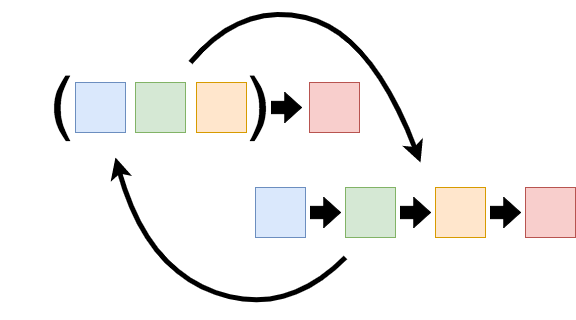
Это процесс в функциональном программировании при котором мы можем трансформировать функцию с несколькими аргументами в упорядоченную последовательность вложенных друг в друга уже других функций. Она возвращает новую функцию, которая ожидает уже следующий аргумент.
Она будет отдавать новую функцию до тех пор, пока не закончится количество аргументов. Аргументы остаются доступными в области видимости и используются при запуске кода, когда завершающая функция в цепочке каррирования отдаётся и запускается.
Каррирование это процесс превращения функции с множественной арностью в функцию с меньшей арностью — Кристина Брэйнвэйв.
Обратите внимание, что термин арность относится напрямую к количеству аргументов которое берет функция. Для примера,
function fn(a, b) {
//...
}function _fn(a, b, c) {
//...
}
У функции fn два аргумента (2х арная функция), а _fn имеет три аргумента(3х арная функция).
Так что каррирование трансформирует функцию с несколькими аргументами в последовательную серию связанных функций, каждая из которых берет один из нужных аргументов.
Давайте посмотрим на простой пример:
function multiply(a, b, c) {
return a * b * c;
}
Функция берёт три аргумента, умножает числа и отдаёт результат.
multiply(1,2,3); // 6
Посмотрите как мы вызвали функцию умножения с полным набором аргументов. Теперь давайте создадим каррированную версию этой функции и посмотрим, как бы мы могли вызвать ту же функцию, но уже через серию запросов:
function multiply(a) {
return (b) => {
return (c) => {
return a * b * c
}
}
}log(multiply(1)(2)(3)) // 6
Мы превратили функцию multiply(1,2,3) в несколько вызовов других вызовов multiply(1)(2)(3).
Просто напросто одна простая функция была переделана в серию последовательных функций. Чтобы получить результат умножения трёх чисел 1, 2 и 3, числа передаются одно за другим, каждое число передаётся следующей функции для запуска.
Мы могли бы разделить multiply(1)(2)(3) на несколько функций, чтобы вы лучше поняли процесс:
const mul1 = multiply(1);
const mul2 = mul1(2);
const result = mul2(3);
log(result); // 6
Давайте рассмотрим всё по последовательности. Мы передали 1 функции multiply:
let mul1 = multiply(1);
Она отдаёт функцию:
return (b) => {
return (c) => {
return a * b * c
}
}
Теперь mul1 это функция с аргументом b.
Далее мы берём функцию mul1, передавая ей 2:
let mul2 = mul1(2);
Mul1 отдаст третью функцию:
return (c) => {
return a * b * c
}
Отданная функция теперь хранится в переменной mul2.
По-сути mul2 будет:
mul2 = (c) => {
return a * b * c
}
Где mul2 вызывается с 3 как параметром,
const result = mul2(3);
Что делает вычисления вместе с параметрами, переданными ранее: a=1, b=2 и получаем 6.
log(result); // 6
Будучи вложенной функцией, mul2 имеет доступ к области видимости других функций, multiply и mul1.
Вот так mul2 будет делать вычисления с переменными указанными в фунциях из которых уже вышли. Хоть функции уже давно и были отданы и зачищены в памяти, но переменные из них ещё остаются доступными.
Вы видите, что три числа были применены одна за другой каждый раз и каждый раз новая функция отдавалась, но до тех пор, пока все числа не иссякнут.
Давайте посмотрим на другой пример:
function volume(l,w,h) {
return l * w * h;
}
const aCylinder = volume(100,20,90) // 180000l
У нас есть функция volume, которая высчитывает объем любой твёрдой формы.
Подход с каррированием будет принимать один аргумент и отдавать функцию, которая также будет принимать ещё один аргумент и отдавать тоже функцию. Это будет продолжаться до последнего аргумента и пока не вернется последняя функция, в которой произойдут уже все операции с умножением предыдущих аргументов вместе с последним.
function volume(l) {
return (w) => {
return (h) => {
return l * w * h
}
}
}
const aCylinder = volume(100)(20)(90) // 180000
Тоже, что и в функции multiply, последняя функция принимает только h, но произведет операции с другими переменными, которые были в уже завершившихся функциях. Это работает вне зависимости от замыканий.
В общем, суть каррирования в том, что мы берём функцию и извлекаем другую функцию, которая отдаёт уже специализированную функцию.
Каррирование в математике
Мне нравится математическая иллюстрация на Википедии, показывающая концепцию каррирования. Давайте посмотрим на неё с нашим собственными примером.
У нас есть уравнение.
f(x,y) = x^2 + y = z
Есть две переменные x и y. Если бы двум переменным было вадано x=3 и y=4, то каким было бы z.
Если мы заменим y на 4 и x на 3 в f(x,y):
f(x,y) = f(3,4) = x^2 + y = 3^2 + 4 = 13 = z
То мы получим результат — 13.
Мы можем каррировать f(x,y), чтобы получить переменные из последовательности функций:
h = x^2 + y = f(x,y) hy(x) = x^2 + y = hx(y) = x^2 + y[hx => w.r.t x] and [hy => w.r.t y]
Если мы поправим x=3 в уравнении hx(y) = x² + y, то оно отдаст новое уравнение у которого есть y как переменная:
h3(y) = 3² + y = 9 + y
Это тоже самое, что и:
h3(y) = 3^2 + y = 9 + y
Значение не было решено, оно отдало новое уравнение 9 + y, ожидая ещё одну переменную y.
Далее мы передадим y=4:
h3(4) = h(3)(4) = f(3,4) = 9 + 4 = 13
y это последняя переменная в цепочке, сложение происходит с предыдущей переменной x=3 и получается 13.
Мы просто напросто каррировали уравнение f(x,y) = 3² + y в последовательность других уравнений.
h3(y) = h(3)(y) = f(3,y) = 3^2 + y = 9 + y
Перед тем как получить результат.
Тут немного математики и вы можете не совсем понять, что там происходит. Почитайте все детали на Википедии.
Каррирование и частичное применение функций
Сейчас некоторые могут подумать, что количество вложенных функций в карированной функции зависит от числа получаемых аргументов. Ну, собственно в карировании так оно и есть.
Сейчас я могу сделать функцию volume таким образом:
function volume(l) {
return (w, h) => {
return l * w * h
}
}
И теперь её можно вызывать так:
const hCy = volume(70);hCy(203,142); hCy(220,122); hCy(120,123);
Или вот так:
volume(70)(90,30);
volume(70)(390,320);
volume(70)(940,340);
Мы только что сделали специальную функцию, которая считает объем любого цилиндрического объекта длинной (l), 70.
Она принимает 3 аргумента и имеет 2 вложенные функции в отличие от предыдущей версии, которой нужно 3 аргумента и у которой 3 вложенные функции.
Но эта версия без каррирования. Там мы просто сделали частичное применение функции volume.
Собственно каррирование и частичное применение схожи, но подразумевают под собой разные концепции.
Частичное применение преобразует функцию в другую функцию с меньшей арностью.
function acidityRatio(x, y, z) {
return performOp(x,y,z)
}
|
V
function acidityRatio(x) {
return (y,z) => {
return performOp(x,y,z)
}
}
Обратите внимание, что тут я оставил в покое детали выполнения функции peroformOp. Она не очень важна. Всё, что вам нужно знать, это концепции применения каррирования и частичного применения.
Это частичное применение функции acidityRatio. Тут нет каррирования. Эта функция частично применена, чтобы получить меньшую арность, ожидая меньшее количество аргументов, чем изначальная функция.
Чтобы применить каррирование, мы могли бы сделать так:
function acidityRatio(x) {
return (y) = > {
return (z) = > {
return performOp(x,y,z)
}
}
}
Каррирование создаёт вложенные функции в соответствии с числом аргументов в ней. Каждая функция тут получает свой аргумент. Если нет аргумента, то нет и каррирования.
Каррирование работает для функций с числом аргументов больше двух — Wikipedia.
Каррирование преобразует функцию в последовательность других функций, каждая из которых берёт по одному аргументу каррированной функции.
Могут быть случаи в которых карррование и частичное применение пересекаются. Предположим, что у нас есть такая функция:
function div(x,y) {
return x/y;
}
Если мы применим частичное применение, то получим вот что:
function div(x) {
return (y) => {
return x/y;
}
}
И каррирование даст нам такой же результат:
function div(x) {
return (y) => {
return x/y;
}
}
Хоть эти два подхода и дают схожий результат, все же по сути они разные.
Как мы раньше говорили, каррирование и частичное применение схожи, но внутри у них всё по-другому. Общее у них то, что при работе они зависят от замыканий.
А каррирование действительно полезно?
Естественно, этот подход очень удобен если вам надо:
Написать небольшие модули кода, которые можно переиспользовать и конфигурировать с легкостью, как и с npm:
Для примера у вас есть магазин и вы хотите дать 10% скидку вашим любимым клиентам:
function discount(price, discount) {
return price * discount
}
Когда один из таких клиентов что-нибудь покупает на 500$, то вы её даёте ему:
const price = discount(500,0.10); // $50
// $500 - $50 = $450
Тут вы понимаете, что этот процесс будет происходить ежедневно:
const price = discount(1500,0.10); // $150 // $1,500 - $150 = $1,350const price = discount(2000,0.10); // $200 // $2,000 - $200 = $1,800const price = discount(50,0.10); // $5 // $50 - $5 = $45const price = discount(5000,0.10); // $500 // $5,000 - $500 = $4,500const price = discount(300,0.10); // $30 // $300 - $30 = $270
Мы можем просто каррировать функцию скидки, чтобы нам не пришлось всегда добавлять 0.10.
function discount(discount) {
return (price) => {
return price * discount;
}
}const tenPercentDiscount = discount(0.1);
Теперь нам нужна только цена для расчета стоимости со скидкой:
tenPercentDiscount(500); // $50
// $500 - $50 = $450
И снова, так получается, что некоторые клиенты уж очень нам важны, важнее других. И мы хотим им дать скидку уже в 20%.
Тут мы будем использовать нашу каррированую функцию скидки:
const twentyPercentDiscount = discount(0.2);
Мы делаем новую функцию для наших очень важных клиентов, вызывая функцию каррирования со значением 0.2, что есть 20%.
Отдаваемая функция twentyPercentDiscount будет использоваться для расчета скидок у таких важных клиентов:
twentyPercentDiscount(500); // 100 // $500 - $100 = $400twentyPercentDiscount(5000); // 1000 // $5,000 - $1,000 = $4,000twentyPercentDiscount(1000000); // 200000 // $1,000,000 - $200,000 = $600,000
Ещё мы можем избегать частых вызовов функций с одним и тем же аргументом:
Для примера, у нас есть функция для расчета объема цилиндрического объекта:
function volume(l, w, h) {
return l * w * h;
}
Так получается, что все они с высотой в 100m. Это приведет к вызову функции с повторяющимся аргументом h = 100.
volume(200,30,100) // 2003000l
volume(32,45,100); //144000l
volume(2322,232,100) // 53870400l
Чтобы решить эту проблему, мы квартируем функцию volume:
function volume(h) {
return (w) => {
return (l) => {
return l * w * h
}
}
}
Теперь мы можем сделать специальную функцию для цилиндров с конкретной высотой:
const hCylinderHeight = volume(100); hCylinderHeight(200)(30); // 600,000lhCylinderHeight(2322)(232); // 53,870,400l
Основа для создания каррирования
Давайте сделаем функцию, которая берёт любую функцию и отдаёт каррированную версию этой функции.
Для этого мы можем сделать так:
function curry(fn, ...args) {
return (..._arg) => {
return fn(...args, ..._arg);
}
}
Что тут произошло? Наша функция каррирования принимает функцию (fn), которую мы хотим, собственно, каррировать и также неизвестное число параметров(…args). Rest оператор используется, чтобы собрать все параметры после fn в …args.
Далее, мы отдаём функцию, которая также собирает все остаточные параметры как …_args. Эта функция вызывает изначальную функцию fn, передавая ей …args и …_args используя spread оператор для параметров, далее значение отдаётся пользователю.
Теперь мы можем использовать нашу собственную функцию для каррирования нужных функций.
Давайте применим эту функцию для создания более специфичной функции по расчёту объёма стометровых цилиндров:
function volume(l,h,w) {
return l * h * w
}
const hCy = curry(volume,100);
hCy(200,900); // 18000000l
hCy(70,60); // 420000l
Заключение
Замыкания делают каррирование возможным. Возможность сохранять состояние уже выполненных функций даёт нам возможность для создания фэктори-функций, которые могут давать точное значение аргументу.
Каррирование очень коварное дело поначалу, учитывая замыкания и функциональное программирование. Но я убеждаю вас, что со временем и постоянной практикой, вы полностью его поймете и увидите всю его ценность.


















