Вопрос на собеседовании о вложении массивов может показаться сложным вначале и очень простым после того, как вы его решите. Но иногда более глубокое погружение в него может раскрыть некоторые дополнительные оптимизации производительности, которые могут быть интересными. После этой статьи вы сможете поразить своих интервьюеров новыми знаниями, о которых они не догадывались!
Что такое проблема вложенности массивов?
Давайте разберемся в самой проблеме.
На вход подается массив arr из целых чисел длины n. Сами целые числа представляют собой некоторую комбинацию индексов. Таким образом, построение входных данных может выглядеть следующим образом:
function scrambleArray(arr) {
const tmpArray = Array.from(arr);
const scrambledArray = new Array(arr.length).fill(1);
let index = 0;
while (tmpArray.length) {
const randomIndex = Math.floor(Math.random() * (tmpArray.length - 1));
scrambledArray[index++] = tmpArray.splice(randomIndex, 1)[0];
}
return scrambledArray;
}
Для каждого члена скремблированного массива необходимо вычислить ряд, который выглядит следующим образом:
s[k] = [arr[k], arr[arr[k]], arr[arr[k]], …].
Правило остановки — когда вы дойдете до числа, которое вы уже посетили, не включайте его.
В конечном итоге вы должны вернуть самую длинную серию в s.
Пример вложенности массива
Возьмем следующие входные данные: [6, 5, 7, 8, 0, 4, 3, 2, 1, 9].
Из этого массива создаются следующие серии:
[3, 8, 1, 5, 4, 0, 6], [4, 0, 6, 3, 8, 1, 5], [2, 7], [1, 5, 4, 0, 6, 3, 8], [6, 3, 8, 1, 5, 4, 0], [0, 6, 3, 8, 1, 5, 4], [8, 1, 5, 4, 0, 6, 3], [7, 2], [5, 4, 0, 6, 3, 8, 1], [9]
Отсюда легко увидеть, что длина самой длинной серии равна 7.
Как решить проблему вложенности массивов на собеседовании?
Решая задачу на собеседовании, вы обычно следуете следующей схеме:
Решить задачу грубой силой
Оптимизировать решение
Давайте последуем этой схеме.
Brute Force
Алгоритм нашего решения довольно прост:
function getNestedArraysMaxLength(inputArray) {
let maxLength = -Infinity;
inputArray.forEach(value => {
const seriesLength = findSeriesLength(inputArray, value);
maxLength = Math.max(seriesLength, maxLength);
});
return maxLength;
}
Мы делаем именно так, как нас попросили. Для каждого члена в inputArray мы получаем его seriesLength и сохраняем найденную максимальную длину. В итоге мы возвращаем максимальную длину, как и просили.
Теперь нам осталось реализовать findSeriesLength:
function findSeriesLength(arr, nextValue) {
const series = {[nextValue]: true};
while (true) {
nextValue = arr[nextValue];
if (series[nextValue]) {
return Object.keys(series).length;
}
series[nextValue] = true;
}
}
Это более сложная часть алгоритма. Он получает массив и следующее значение (которое является первым значением в серии). Серия всегда включает первое число, поэтому мы устанавливаем его в серию. Затем мы заполняем серию, пока снова не дойдем до того же числа. Как только мы это сделаем, мы возвращаем длину серии.
Сложность решения методом перебора составляет O(n*n) (O n в квадрате). Это потому, что в худшем случае мы могли бы перебрать все числа в исходном массиве и для каждого из них перебрать их снова, когда будем составлять серию. Обычно, в интервью, мы можем сделать лучше.
Оптимизация по времени
Если посмотреть на пример, показанный выше, можно обнаружить закономерность:
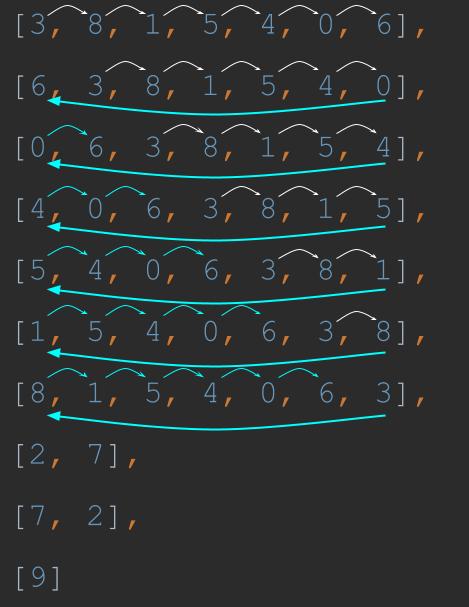
Рисунок 1: Закономерность в числах. Эта иллюстрация демонстрирует цикличность нашего ряда. Первый начинается с трех и проходит весь путь до 6 (белые стрелки). Следующий начинается с 6, затем с 3 и проходит тот же путь до 0, после которого всегда идет 6 (синяя стрелка) и так далее.
Рисунок 1 иллюстрирует циклический характер серий. Серии — это просто циклы одних и тех же чисел. Мы можем использовать это для оптимизации нашего алгоритма. Давайте добавим массив памяти для хранения подсчета значений, которые мы уже встречали:
function getNestedArraysMaxLength(inputArray) {
let maxLength = -Infinity;
const memory = [];
inputArray.forEach(value => {
memory[value] = findSeriesLength(inputArray, value, memory);
maxLength = Math.max(maxLength, memory[value]);
});
return maxLength;
}
function findSeriesLength(arr, nextValue, memory) {
const series = {[nextValue]: true};
while (true) {
nextValue = arr[nextValue];
if (memory[nextValue]) {
return memory[nextValue];
}
if (series[nextValue]) {
return Object.keys(series).length;
}
series[nextValue] = true;
}
}
Давайте перечислим различия:
В строке 3 определяется массив памяти.
Строка 6 добавляет значение count в массив памяти вместо того, чтобы хранить его в переменной. Теперь мы используем это значение в строке 7 вместо переменной seriesLength.
Теперь findSeriesLength использует полученную память в качестве входных данных, чтобы проверить, есть ли у нас уже счетчик для определенного значения (строки 18-20).
Давайте посмотрим на сложность (большое O) этого решения. Мы по-прежнему перебираем n значений в массиве inputArray. Но для каждого цикла, как показано на рисунке 1, мы пройдем только один раз. Наша временная сложность теперь O(n) (линейная), потому что единственное место, где мы перебираем n элементов, — это главный цикл forEach. Наша пространственная сложность теперь O(n), потому что теперь мы используем вспомогательный массив памяти.
Бенчмаркинг
Давайте посмотрим на разницу между оптимизированным и неоптимизированным алгоритмами. Мы будем использовать сайт jsben.ch для оценки производительности. Наш бенчмарк начнется с n = 10 (да, я знаю, что это мало, но потерпите, пожалуйста).
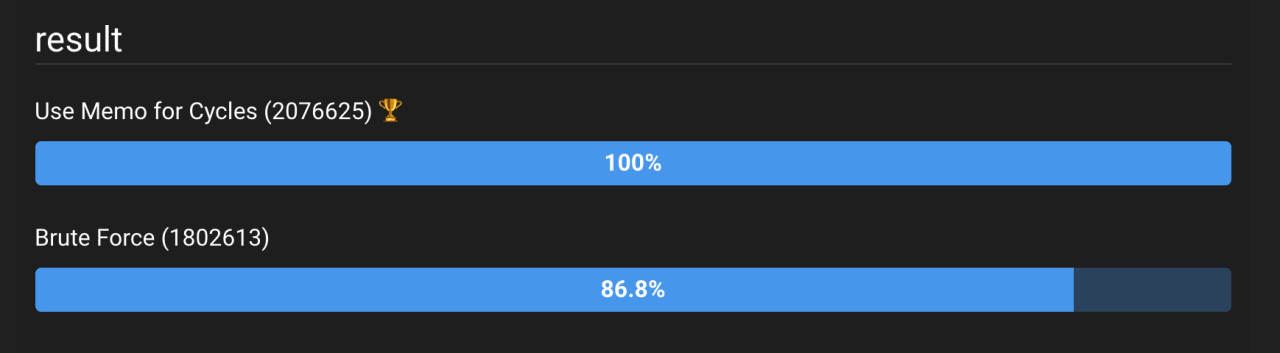
Рисунок 2: Результаты многократного выполнения двух решений. Видно, что решение, использующее памятку для циклов, оказалось примерно на 15% лучше.
Рисунок 2 (живой бенчмарк можно посмотреть здесь: https://jsben.ch/GQld2) показывает, что оптимизация сработала. Хотя… мы ожидали гораздо большего улучшения, не так ли? Мы улучшили сложность на много!
Можем ли мы оптимизировать больше?
Есть несколько способов оптимизировать наш алгоритм. Для начала давайте посмотрим, что произойдет, если мы используем счетчик вместо массива серий в функции findSeriesLength. Мы изменим функцию следующим образом:
function findSeriesLength(arr, nextValue) {
const startingNumber = nextValue;
let count = 1;
while (true) {
nextValue = arr[nextValue];
if (startingNumber === nextValue) {
return count;
}
count++;
}
}
В приведенном выше коде вместо создания серии, которая не нужна для нашей задачи (нам нужно вернуть только длину), мы запоминаем первое значение (startingNumber) и создаем счетчик.
Эталон для этой функции показан на рисунке 3 (живая версия здесь).
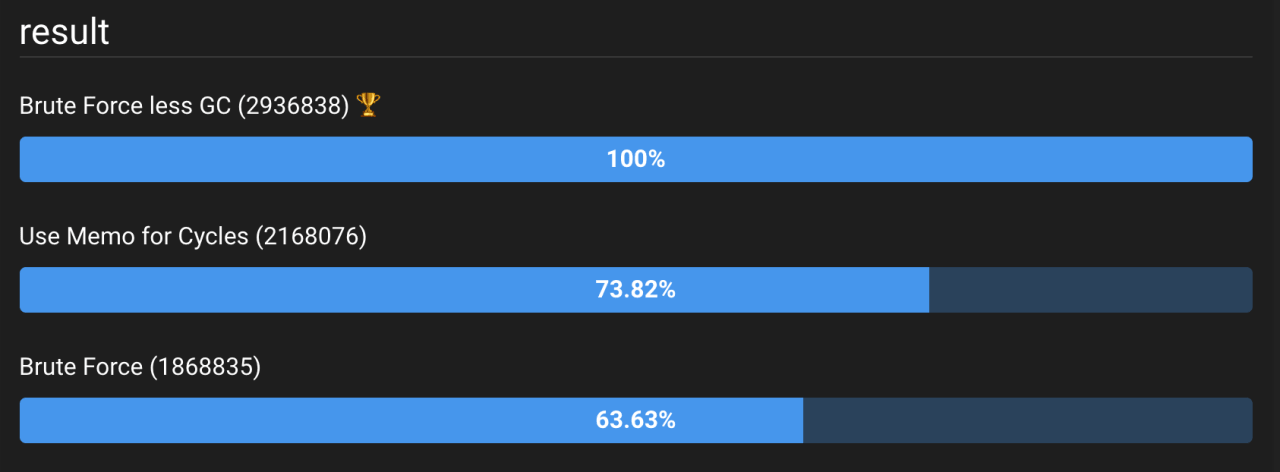
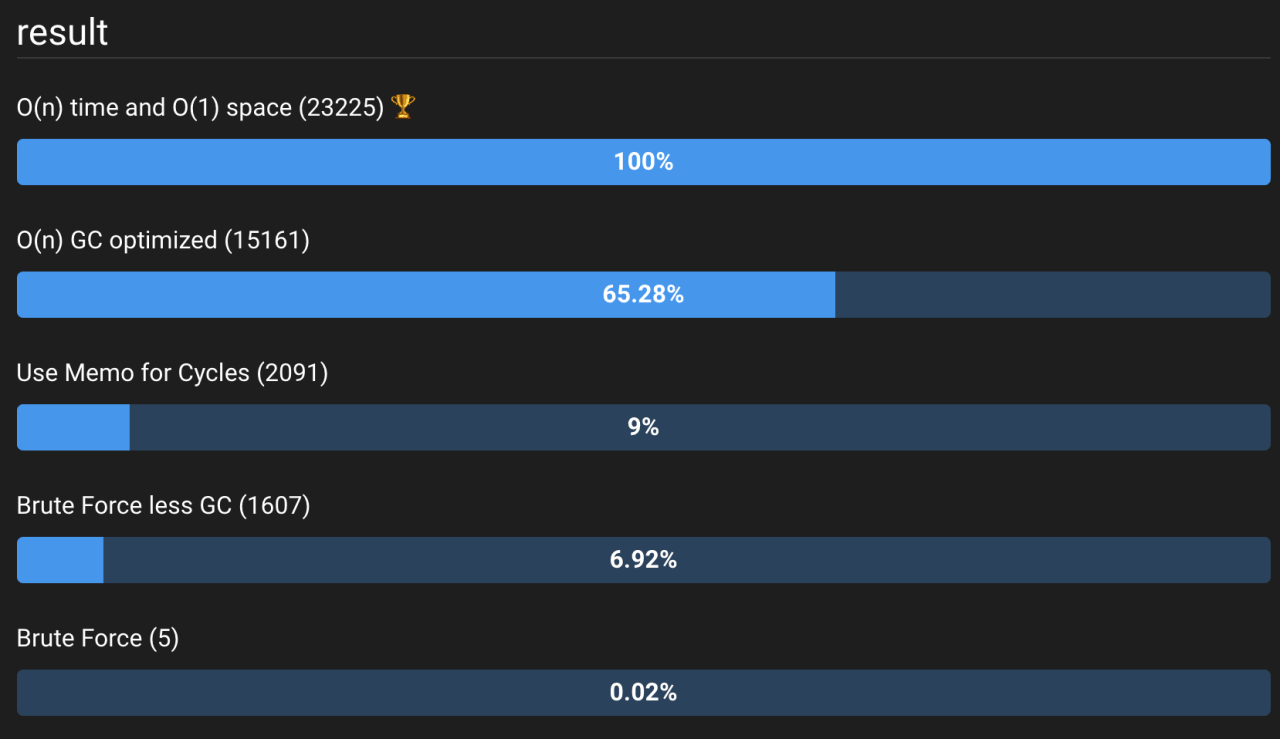
Рисунок 3: Результаты бенчмаркинга Brute Force со счетчиком (Brute Force less GC) против Brute Force и оптимизированного алгоритма (Use Memo for Cycles). Это привело к значительному сокращению сборки мусора, что сделало брутфорс O(n*n) еще более эффективным, чем алгоритм O(n).
Что бы сделала та же оптимизация с оптимизацией сложности? Результаты, показанные на рисунке 4, могут вас удивить.
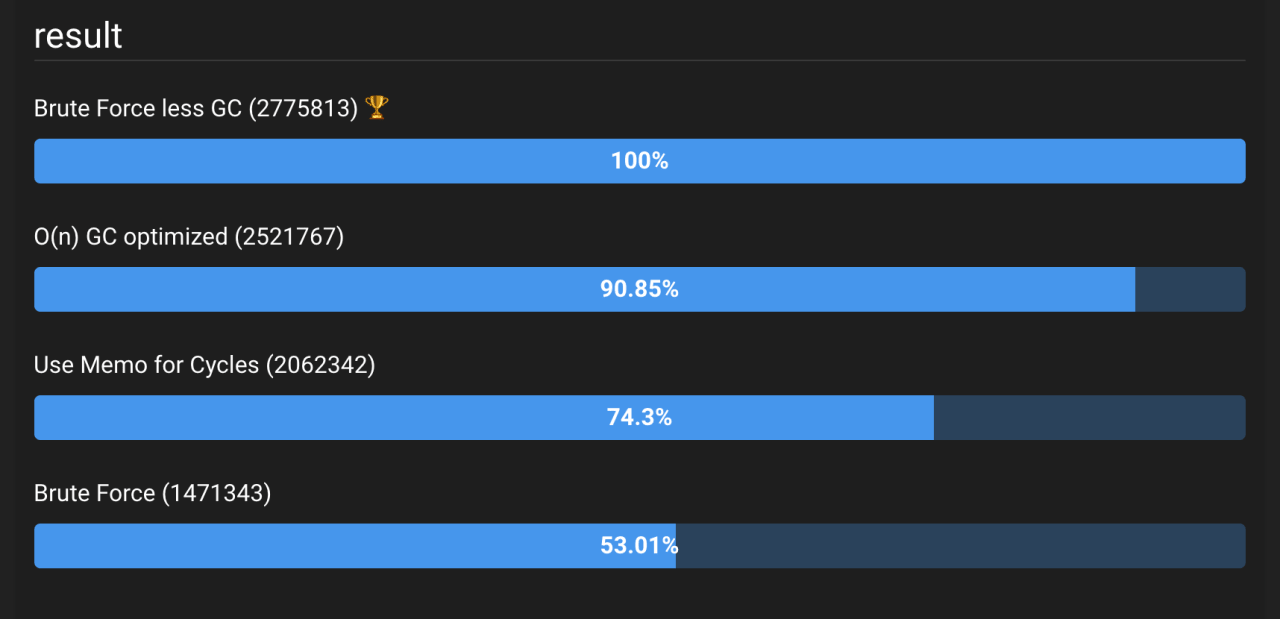
Рисунок 4: Результаты сравнения O(n) и O(n*n) с оптимизированной функцией findSeriesLength. О и вот — алгоритм O(n) работает медленнее, чем Brute Force!!! Посмотреть код.
Что здесь происходит? Может ли алгоритм грубой силы O(n*n) работать быстрее, чем алгоритм O(n)?
Сборка мусора (сокращенно GC) является основным фактором производительности JavaScript. Если функция создает и уничтожает большое количество объектов/массивов, это влечет за собой дополнительные расходы: выделение памяти и сборку мусора. Движок JS должен выделять память для ваших объектов и массивов. JS-движок также очищает отброшенные объекты и массивы (сборка мусора). Эти процессы занимают время. В масштабе — еще больше.
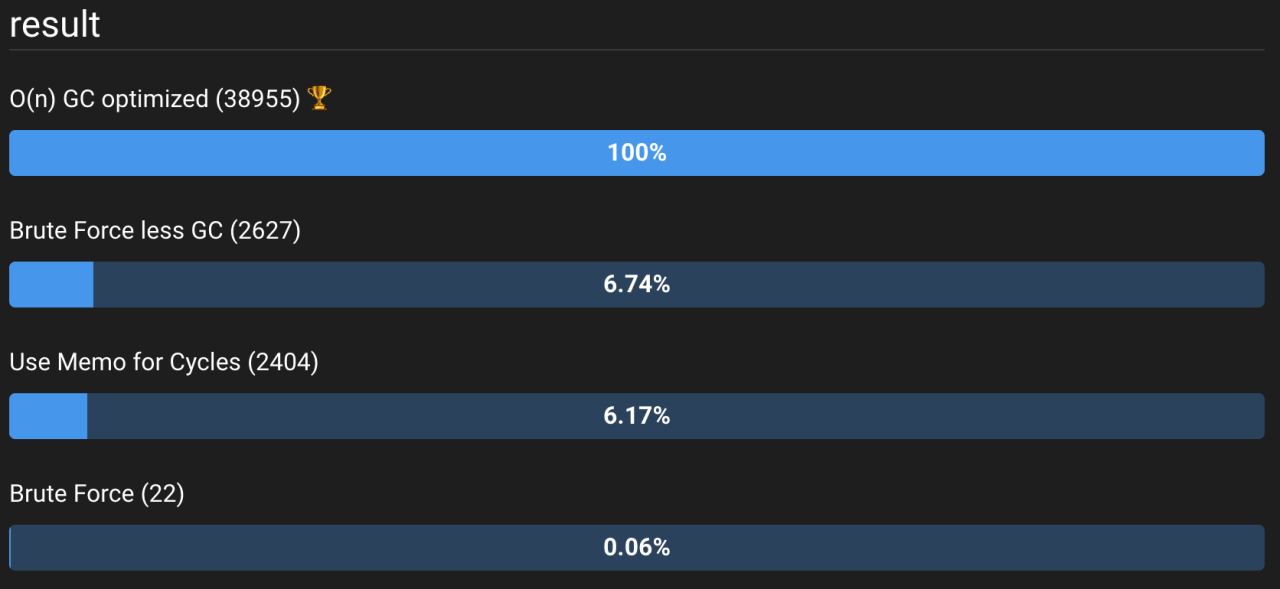
Кроме того, алгоритм O(n), как показано здесь, не дает тех преимуществ, которые мы ожидаем от гораздо более эффективного алгоритма. Это потому, что у нас очень низкое n. Если мы увеличим n до 1000, то увидим другую картину. На рисунке 5 показаны результаты для n = 1000.
Рисунок 5: Тот же код, но на этот раз входной массив имеет длину 1000. Посмотрите демонстрацию в реальном времени здесь.
Таким образом, здесь мы узнаем две вещи:
Улучшение сложности хорошо для больших n.
GC может быть основным узким местом в вашем JavaScript-коде.
Оптимизация по времени и пространству
Мы также можем улучшить временную сложность без увеличения пространственной сложности и полностью избежать накладных расходов на GC.
Вместо того чтобы создавать массив памяти, мы можем просто установить маркер внутри нашего массива:
function getNestedArraysMaxLength(inputArray) {
let maxLength = -Infinity;
inputArray.forEach((value, index) => {
const seriesLength = findSeriesLength(inputArray, index);
maxLength = Math.max(maxLength, seriesLength);
});
return maxLength;
}
function findSeriesLength(arr, nextIndex) {
let count = 0;
while (true) {
let nextValue = arr[nextIndex];
if (nextValue === null) {
return count;
}
arr[nextIndex] = null;
nextIndex = nextValue;
count++;
}
}
Обратите внимание, что мы убрали любое упоминание о памяти. Хитрость здесь заключается в том, чтобы установить каждое значение, которое мы уже передали, как null (или какое-то другое известное значение). Тогда каждый раз, когда мы натыкаемся на null, мы знаем, что уже проверили этот цикл, и нет необходимости идти дальше.
Результаты, показанные на рисунке 6, весьма убедительны. Использование O(n) по времени и улучшение до O(1) по пространству также привело к лучшей производительности. Мы уже знаем причину этого — выделение памяти и сборка мусора. Когда мы не выделяем массив памяти, мы фактически уменьшаем объем выделяемой памяти и тем самым уменьшаем количество циклов GC.
Рисунок 6: Сравнение всех алгоритмов до сих пор с улучшением O(n) по времени и O(1) по пространству. Посмотреть живые тесты можно здесь.
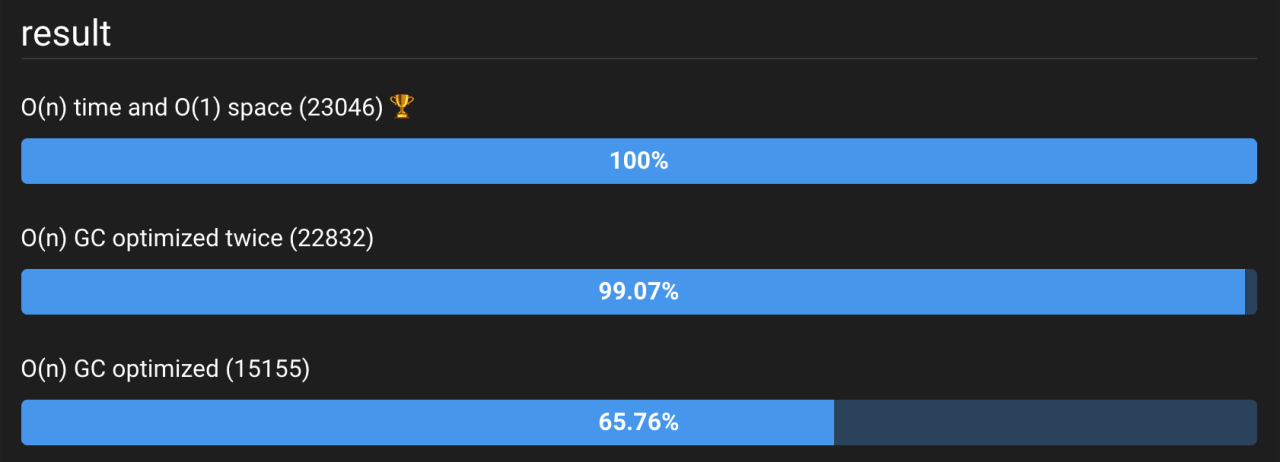
Чтобы доказать нашу гипотезу, мы можем легко убрать GC из решения для пространства O(n). Изменив строку const memory = []; на const memory = new Array(inputArray.length).fill(1); мы предварительно распределим память перед запуском функции и, таким образом, получим гораздо меньше циклов GC и запросов на распределение памяти. Смотрите результаты на рисунке 7.
Рисунок 7: Результаты оптимизации O(n) — динамическое выделение памяти (внизу) занимает значительно больше времени, чем предварительное выделение памяти (в середине). Предварительное распределение памяти занимает примерно столько же времени, сколько и полностью оптимизированный код. Пример кода здесь.
Есть ли что-нибудь еще?
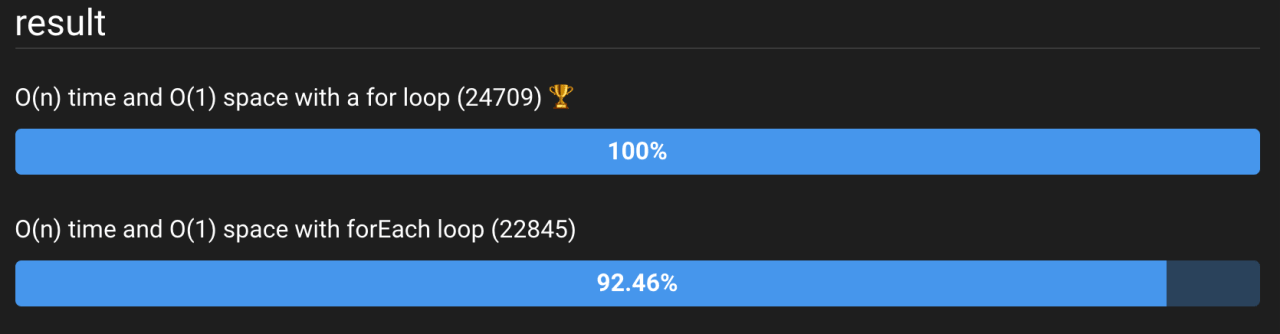
Конечно! Но с этого момента, вероятно, это будет микро оптимизация, которая зависит от браузера, который вы используете, или JS движка, который вы используете. Например, если мы заменим forEach на цикл for, мы увидим следующее улучшение:
Рисунок 8: Результаты микрооптимизации — замена цикла forEach на цикл for. Мы видим небольшое увеличение производительности. Это может зависеть от браузера и JS-движка. Посмотреть пример кода можно здесь.
Итог:
Задача «Вложенности массивов» — это относительно простая проблема на собеседовании. Ее решение методом перебора довольно простое, а оптимизация проста: либо сохранение в памяти старых результатов (мемоизация), либо использование флага на самих данных.
Мы также увидели, что способ обработки данных может повлиять на скорость решения. Распределение памяти и сборка мусора оказывают большое влияние на производительность вашего кода.
Наконец, мы увидели, что некоторые оптимизации, получившие популярность благодаря своему «забавному факту» и довольно известному характеру (например, замена forEach), с меньшей вероятностью дадут вам лучшую производительность.
Для нашей задачи — извлечения самой длинной серии — наша обработка данных была оптимизирована так, как мы это делали. Мы либо вели счетчик, либо предварительно выделяли массив памяти.
Я надеюсь, что теперь, если вам зададут этот вопрос на собеседовании, вы сможете увлечь интервьюера глубокими объяснениями о распределении памяти и сборке мусора, после того как закончите объяснять очевидную сложность big O.