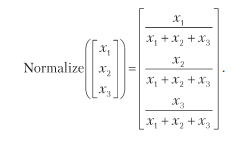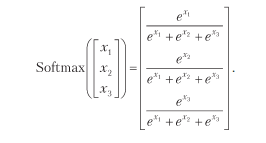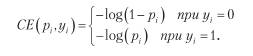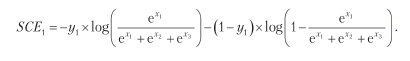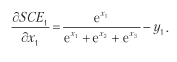Книга «Глубокое обучение: легкая разработка проектов на Python»

В этой книге:

• Четкие схемы, помогающие разобраться в нейросетях, и примеры рабочего кода.
• Методы реализации многослойных сетей с нуля на базе простой объектно-ориентированной структуры.
• Примеры и доступные объяснения сверточных и рекуррентных нейронных сетей.
• Реализация концепций нейросетей с помощью популярного фреймворка PyTorch.

Расширения

Из первых трех глав мы узнали, что такое модели глубокого обучения и как они должны работать, а затем создали первую модель глубокого обучения и научили ее решать относительно простую задачу прогнозирования цен на жилье на основе некоторых признаков. Однако в реальных задачах успешно обучить модели глубокого обучения не так просто. В теории такие модели действительно позволяют найти оптимальное решение любой задачи, которую можно свести к обучению с учителем, но вот на практике не все так просто. Теория говорит о том, что данная архитектура модели позволяет найти оптимальное решение проблемы. Однако помимо теории есть хорошие и понятные методы, которые повышают вероятность удачного обучения нейронной сети, и эта глава именно об этом.

Начнем с математического анализа задачи нейронной сети: поиска минимума функции. Затем покажем ряд методов, которые помогут выполнить эту задачу, на классическом примере с рукописными цифрами. Мы начнем с функции потерь, которая используется в задачах классификации в глубоком обучении, и продемонстрируем, что она значительно ускоряет обучение (пока мы говорили только о регрессии, а функцию потерь и задачу классификации не рассматривали). Рассмотрим новые функции активации и покажем, как они влияют на обучение, а также поговорим об их плюсах и минусах. Далее рассмотрим самое важное (и простое) улучшение для уже знакомого нам метода стохастического градиентного спуска, а также кратко поговорим о возможностях продвинутых оптимизаторов. В заключение мы рассмотрим еще три метода улучшения работы нашей системы: снижение скорости обучения, инициализация весов и отсев. Как мы увидим, все эти методы помогут нашей нейронной сети находить оптимальные решения.

В первой главе мы сначала приводили рисунок со схемой, затем математическую модель, и потом код для рассматриваемой концепции. В этой главе какой-то конкретной схемы у методов не будет, поэтому мы сначала дадим краткое описание метода, а затем перейдем к математике (которая будет намного проще, чем в первой главе). Завершим рассмотрение кодом, который реализует метод с использованием введенных нами ранее строительных блоков. Итак, начнем с краткого описания задачи нейронной сети: поиска минимума функции.

Немного о понимании нейронных сетей

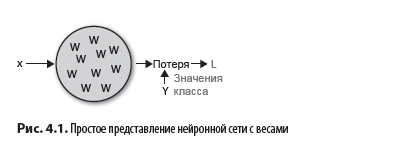
Как мы уже видели, в нейронных сетях содержатся весовые коэффициенты, или веса. Значения весов и входные данные X и y позволяют вычислить «потери». На рис. 4.1 показана схема описанной нейронной сети.

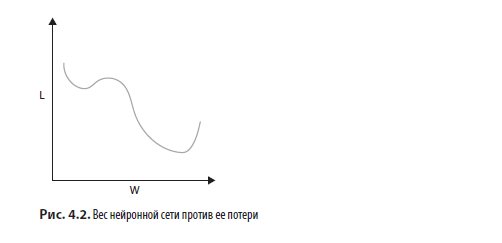
На самом деле каждый отдельный вес имеет некоторую сложную нелинейную связь с характеристиками X, целью y, другими весами и, в конечном счете, потерей L. Если мы построили график, варьируя значение веса, сохраняя постоянными значения с другими весами, X и y, и вычерчивая полученное значение потери L, мы могли видеть что-то вроде того, что показано на рис. 4.2.

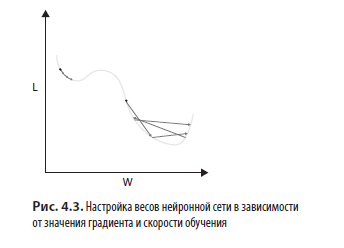
Запуская обучение нейронной сети, мы задаем весам начальные значения в пределах, показанных на рис. 4.2. Затем, используя градиенты, которые рассчитываем во время обратного распространения, мы итеративно обновляем значения весов, основываясь на наклоне кривой и текущем значении веса. На рис. 4.3 показана геометрическая интерпретация настройки весов нейронной сети в зависимости от градиента и скорости обучения. Слева стрелками показано, что это правило применяется многократно с меньшей скоростью обучения, чем в области справа. Обратите внимание, что в обоих случаях изменение значения пропорционально наклону кривой при данном значении веса (более крутой наклон означает более сильное изменение).

Конечная цель обучения модели — задать весам такие значения, чтобы значение потерь нашло глобальный минимум. Как видно из рис. 4.3, если шаг обучения слишком мал, мы рискуем попасть в локальный минимум, который будет менее оптимален, чем глобальный (этот сценарий показан синими стрелками). Если шаг слишком велик, мы рискуем «перепрыгнуть» глобальный минимум, даже если находимся рядом с ним (этот сценарий показан красными стрелками). Это самая главная дилемма настройки скорости обучения: слишком малая скорость ведет к попаданию в локальный минимум, а слишком большая ведет к промаху.

На деле все еще сложнее. В нейронной сети могут быть тысячи, а может, и миллионы весов, и в этом случае мы ищем глобальный минимум в тысяче- или миллионмерном пространстве. Более того, поскольку мы на каждой итерации будем обновлять значения весов, а также передавать различные значения X и y, сама кривая, на которой мы ищем минимум, тоже постоянно меняется! Из-за этого нейронные сети много лет были объектом споров и скепсиса, так как казалось, что оптимальное решение найти невозможно. Ян Лекун и соавт. в статье 2015 года высказались следующим образом:

На рис. 4.3 хорошо видно, почему скорость обучения не должна быть слишком большой или слишком маленькой, отсюда интуитивно понятно, почему приемы, которые мы собираемся изучить в этой главе, действительно работают. Теперь, понимая цель нейронных сетей, мы приступим к работе. Начнем с многопеременной логистической активационной функции кросс-энтропийных потерь, которая работает в значительной степени благодаря своей способности обеспечивать более крутые градиенты весов, чем функция среднеквадратичных потерь, которую мы видели в предыдущей главе.

Многопеременная логистическая функция активации с перекрестно-энтропийными потерями

В главе 3 в качестве функции потерь мы использовали среднеквадратическую ошибку (MSE). Функция обладала свойством выпуклости, то есть чем дальше прогноз от цели, тем круче был бы начальный градиент, который класс Loss отправлял обратно в слои сети. Из-за этого увеличивались градиенты, полученные параметрами. Но оказывается, что в задачах классификации это не предел мечтаний, поскольку в этом случае значения, которые выводит наша сеть, должны интерпретироваться как вероятности в диапазоне от 0 до 1, и вектор вероятностей должен иметь равную 1 сумму для каждого наблюдения, которое мы передали через нашу сеть. Многопеременная логистическая функция активации (будем использовать сокращенное английское название — softmax) с перекрестно-энтропийными потерями позволяет за счет этого получить более крутые градиенты, чем средний квадрат ошибки, при тех же входных данных. У этой функции два компонента: первый — это функция softmax, а второй — это перекрестно-энтропийные потери. Рассмотрим их подробнее.

Компонент № 1: функция softmax

Для задачи классификации с N возможными категориями нейронная сеть выдаст вектор из N значений для каждого наблюдения. Для задачи с тремя категориями вектор может быть таким:

Математическое представление

Поскольку речь идет о задаче классификации, мы знаем, что результат следует интерпретировать как вектор вероятностей того, что данное наблюдение относится к категории 1, 2 или 3 соответственно. Один из способов преобразования этих значений в вектор вероятностей — нормализация, сложение и деление на сумму:

Но есть способ, который дает более крутые градиенты и имеет пару тузов в рукаве, — softmax. Эта функция для вектора длины 3 будет иметь вид:

Наглядное представление

Суть функции softmax заключается в том, что она усиливает максимальное значение по сравнению с другими, заставляя нейронную сеть стать «чувствительнее» к прогнозам в задаче классификации. Давайте сравним результаты функций normalize и softmax для данного выше вектора вероятностей:

normalize(np.array([5,3,2]))
array([0.5, 0.3, 0.2])
softmax(np.array([5,3,2]))
array([0.84, 0.11, 0.04])

Видно, что исходное максимальное значение 5 выделилось сильнее, а два других стали ниже, чем после нормализации. Таким образом, функция softmax — это нечто среднее между нормализацией значений и фактическим применением функции max (которая в данном случае приведет к выводу массива ([1.0, 0.0, 0.0])), отсюда и название «softmax» — «мягкий максимум».

Компонент № 2: перекрестно-энтропийная потеря

Напомним, что любая функция потерь берет на вход вектор вероятностей

и вектор фактических значений

Математическое представление

Функция перекрестно-энтропийной потери для каждого индекса i в этих векторах:

Наглядное представление

Чтобы понять, чем такая функция потерь хороша, отметим, что, поскольку каждый элемент y равен 0 или 1, предыдущее уравнение сводится к:

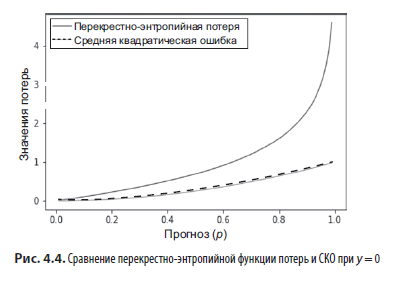
Теперь все проще. Если y = 0, то график зависимости значения этой потери от значения среднеквадратичной потери на интервале от 0 до 1 выглядит так, как показано на рис. 4.4.

Штрафы у перекрестно-энтропийной функции потерь намного выше, и кроме того, они становятся больше с увеличением скорости, стремясь к бесконечности, когда разница между нашим прогнозом и целью стремится к 1! График для случая у = 1 похож, только «перевернут» (то есть он повернут на 180 градусов вокруг линии х = 0.5).

Таким образом, для задач, где результат должен лежать между 0 и 1, перекрестно-энтропийная функция потерь создает более крутые градиенты, чем MSE. Но настоящая магия происходит, когда мы объединяем эту функцию потерь с функцией softmax — сначала проводим выход нейронной сети через функцию softmax, чтобы нормализовать его до нужного диапазона, а затем подаем полученные вероятности в перекрестно-энтропийную функцию потерь.

Давайте посмотрим, как это выглядит в сценарии с тремя категориями, который мы уже упоминали. Выражение для компонента вектора потерь i = 1, то есть первого компонента потерь для данного наблюдения, которое мы обозначим как

имеет вид:

Это выражение дает более сложный градиент для данной функции потерь. Но есть более элегантное выражение, которое легко и записать, и реализовать:

Это означает, что полный градиент перекрестно энтропийной функции с softmax равен:

Готово! Как и было обещано, итоговая реализация тоже будет простой:

softmax_x = softmax(x, axis = 1)
loss_grad = softmax_x — y

Об авторе

Сет Вейдман — data scientist, несколько лет практиковал и преподавал основы машинного обучения. Начинал как первый специалист по данным в Trunk Club, где создавал модели оценки потенциальных клиентов и системы рекомендаций. В настоящее время работает в Facebook, где создает модели машинного обучения в составе команды по инфраструктуре. В промежутках преподавал Data Science и машинное обучение на буткемпах и в команде по корпоративному обучению в компании Metis. Обожает объяснять сложные концепции, стремясь найти простое в сложном.

Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок

Для читателей Bookflow скидка 25% по купону — Глубокое обучение