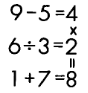102 задачи на логику и смекалку для детей и взрослых.
102 задачи на логику и сообразительность. Решение задач на логику это замечательное упражнение как для детей, так и взрослых, которое развивает изобретательность и нестандартность мышления. Некоторые из приведенных ниже подходят даже дошкольникам. Ответы к загадкам прилагаются.
1. В 12-этажном доме есть лифт. На первом этаже живет всего 2 человека, от этажа к этажу количество жильцов увеличивается вдвое. На каком этаже в этом доме чаще других нажимается кнопка вызова лифта?
2. Джордж Вашингтон, Шерлок Холмс, Уильям Шекспир, Людвиг Ван Бетховен, Наполеон Бонапарт и Нерон — кто из них принципиально отличается от других?
3. Это известная старинная задача, где крестьянину нужно перевести через реку волка, козла и капусту. Лодка такая маленькая, что в ней кроме крестьянина может поместиться еще только один (пассажир). Но если оставить волка с козлом, то волк его съест, если оставить козла с капустой, то будет съедена капуста. Как быть крестьянину?
4. Кузнецу принесли пять цепей, по три кольца в каждой, и поручили соединить их в одну цепь. Кузнец решил вскрыть четыре кольца и снова их заковать. Нельзя ли выполнить ту же работу, вскрыв меньше колец?
5. Жили четыре друга. Они имели имена Альберт, Карл, Дитрих и Фридрих. Фамилии друзей те же, что и имена, только так, что ни у кого из них имя и фамилия не были одинаковыми, кроме того, фамилия Дитриха не Альберт. Определите фамилию и имя каждого мальчика, если известно, что имя мальчика, у которого фамилия Фридрих, есть фамилия того мальчика, имя которого — фамилия Карла.
6. Что не может увеличить лупа в треугольнике?
7. Рядом с берегом стоит корабль со спущенной на воду веревочной лестницей, которая имеет 10 ступенек. Расстояние между ними 30 см. Самая нижняя ступенька касается поверхности воды. Океан сегодня очень спокойный, но начинается прилив, поднимающий воду за час на 15 см. Через сколько часов покроется водой третья ступенька веревочной лестницы?
8. Три любителя водного спорта имеют одну лодку. Они изобрели способ, чтобы никто из посторонних не мог ее украсть. Для этого они держат ее на цепи, которая запирается тремя замками. Каждый из любителей имеет только один ключ (все ключи от разных замков), но все-таки он может взять лодку, используя один только свой ключ. Как же у них это получается?
9. Двое туристов одновременно вышли из пункта А и пошли в пункт В. Первый турист половину времени, затраченного им на переход, шел со скоростью 5 км/ч, а затем пошел со скоростью 4 км/ч. Второй же первую половину пути прошел по 4 км/ч, а затем пошел по 5 км/ч. Кто из них раньше пришел в пункт B?
10. Есть квадратный пруд (см. схематический рисунок). По углам его у воды растут четыре старых дуба. Пруд понадобилось расширить, сделав его вдвое больше по площади, сохраняя, однако, квадратную форму. Но старые дубы трогать не желают. Выполнима ли эта задача?

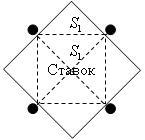
11. Василию, Петру, Семену и их женам Наталье, Ирине, Анне вместе 151 год. Каждый мужчина старше своей жены на 5 лет. Василий на 1 год старше Ирины. Наталье и Василию вместе 48 лет, Семену и Наталье вместе 52 года. Кто на ком женат, сколько кому лет? (Возраст должен быть выражен в целых числах.)
12. Василию, Петру, Семену и их женам Наталье, Ирине, Анне вместе 151 год. Каждый мужчина старше своей жены на 5 лет. Василий на 1 год старше Ирины. Наталье и Василию вместе 48 лет, Семену и Наталье вместе 52 года. Кто на ком женат, сколько кому лет? (Возраст должен быть выражен в целых числах.)
13. Вы заболели, пошли к врачу который дал вам по три таблетки в баночках А и В. Таблетки идентичны внешне, но имеют разный эффект. Вы должны каждый день выпивать вместе таблетку из баночки А и таблетку из баночки В, так в течение трех дней. Рецепт нельзя нарушать. Но утром после первого дня вы увидели, что на столе лежат три таблетки, баночка В пустая, а в баночке А только одна таблетка. Как вам действовать, чтобы закончить лечение не нарушая рецепта?
14. Человек рассматривает портрет. «Чей это портрет вы рассматриваете?» — спрашивают у него, и человек отвечает: «В семье я рос один, как перст, один. И все-таки отец того, кто на портрете, — сын моего отца». Чей портрет рассматривает человек?
15. Человек рассматривает портрет. «Чей это портрет вы рассматриваете?» — спрашивают у него, и человек отвечает: «В семье я рос один, как перст, один. И все-таки отец того, кто на портрете, — сын моего отца». Чей портрет рассматривает человек?
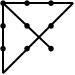
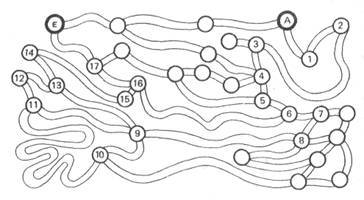
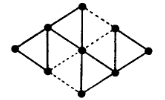
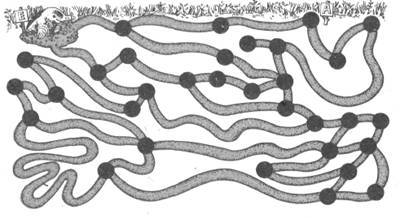
16. В один стакан налито вино, а в другой — такое же количество воды. Из стакана с вином берут чайную ложку вина и переливают ее в стакан с водой. Затем, хорошо перемешав содержимое стакана с водой, берут чайную ложку раствора и переливают ее обратно в стакан с вином. Чего при этом оказывается больше — вина в воде или воды в вине?
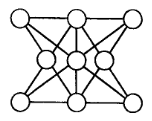
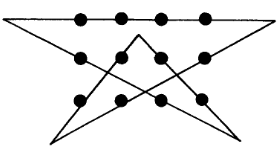
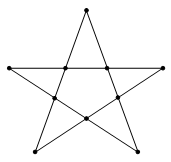
17. Соединить все точки на рисунке 4-мя прямыми отрезками.
18. Что больше: сумма всех цифр или их произведение?
19. В кармане лежат две монеты на общую сумму 15 копеек. Одна из них не пятак. Что это за монеты?
20. Два города, А и В, находятся на расстоянии 30 км друг от друга. Из этих городов одновременно выходят друг другу навстречу два пешехода и движутся, не останавливаясь, каждый со скоростью 5 км/ч. Но вместе с первым пешеходом из города А вылетает муха, которая пролетает за час 10 км. Муха опережает первого пешехода и летит навстречу второму, вышедшему из B. Встретив его, она сразу поворачивает обратно к пешеходу A. Встретив его, снова летит обратно навстречу пешеходу В, и так продолжала она свои полеты вперед и назад до тех пор, пока пешеходы не встретились. Тогда она успокоилась и села одному из пешеходов на шляпу. Сколько километров пролетела муха?
21. Известно следующее:
1). Фамилии машиниста паровоза, кочегара и кондуктора (но не обязательно в таком же порядке) — Ковалев, Петров, Смирнов.
2). Фамилии пассажиров — доктор Ковалев, доктор Петров, доктор Смирнов.
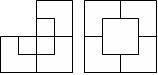
3). Доктор Ковалев живет в А.
4). Кондуктор живет по середине пути от А до В.
5). Пассажир, носящий ту же фамилию, что и кондуктор, живет в В.
6). Доктор Петров зарабатывает ежемесячно 25000 рублей.
7). Пассажир, живущий очень близко от кондуктора, зарабатывает ровно в 3 раза больше, чем кондуктор.
8). Смирнов выиграл партию в шахматы у кочегара.
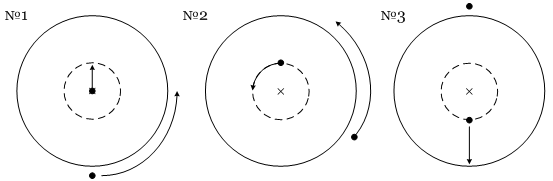
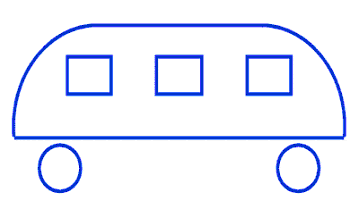
Какая фамилия машиниста
22. Лишь на три минуты в день заглядывает пламенный глаз бога солнца Ра в святилище богини Изиды. Огромное зеркало собирает свет, превращая его в жар, и жрецы выпекают на драгоценном масле жертвенные лепешки из белой пшеницы. На жаровне помещается лишь два коржа, но хотя и раскаленная она, даже в солнечном пламени нужна целая минута, чтобы пропечь оба коржа с одной стороны. А приготовить нужно непременно три лепешки — по одной каждому из главных богов: солнечному Ра, мрачной Изиде и могущественному Осирису. Как справиться с этой задачей?
23. На ветке сидели три птички, две решили улететь. Сколько осталось сидеть на ветке птичек?
24. Что можно взять в левую руку, но нельзя взять в правую?
25. Пусть фигура состоит из трех равных квадратов, расположенных так, как показано на рисунке. Вырежьте из этой фигуры такую часть, чтобы приложив ее к оставшейся части, получить квадрат, внутри которого есть квадратное отверстие.
26. Как измерить диаметр тонкой проволоки, имея в распоряжении лишь карандаш и масштабную линейку?
27. Даны два бикфордовых шнура. Каждый из шнуров горит ровно 1 час. Горение неравномерное, то есть, например, половина может сгореть за пять минут, а другая за 55 минут. Длина может быть разной. Задача: зафиксировать время в 45 минут с помощью этих шнуров.
28. Перед слепым математиком на столе находятся 100 фишек, одна сторона которых белая, другая — черная. Известно, что в начальный момент 10 из них лежат белой стороной вверх, остальные — черной. Каким образом эти фишки можно разделить на 2 группы так, что бы в каждой из них было одинаковое количество белых, или не было вообще?
29. Галина захотела купить одно мороженое, но ей не хватает 6 копеек. Иван также хочет купить одно мороженое, но ему не хватает 1 копейки. Галина и Иван решили вместе купить одно мороженое на двоих, но им все равно не хватает одной копейки. Вопрос: сколько же стоит одно мороженое?
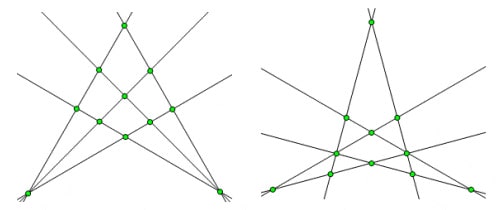
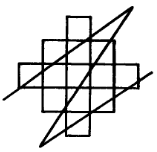
30. Используя 6 прямых линий, создайте 11 пересечений (точек, возникших в результате перерыва линий).
31. Определите в какую сторону едет автобус на рисунке: влево или вправо? Дети из детсада почти мгновенно на нее верно отвечают! А вы уже догадались?
32. Каким должен быть путь, чтобы побывать в каждом квадрате за 15 переходов, начав путь с выделенного квадрата и закончив им. Пересекать пути нельзя!

33. Вы едете в авто и на одной остановке видите трех людей: 1) старушку бабушку, которой немедленно нужно в больницу иначе она умрет, 2) своего старого товарища, который когда-то спас вам жизнь и который опаздывает по очень важному для него делу и 3) девушку (парня) своей мечты. В вашем авто, кроме вашего места есть еще одно (вы не можете взять с собой больше одного человека).
Кого вы выберете, как вы поступите?
34. Мистер Джонс был найден мертвым за письменным столом в своем кабинете. Причина смерти — пулевое ранение в голову. Детектив Бонс, прибывший на место происшествия, среди других предметов обратил внимание на магнитофон, который лежал на столе. Включив магнитофон, он, к своему удивлению, услышал голос мистера Джонса, который сделал следующее заявление: «Говорит Джонс. Только что мне позвонил Смит. Сказал, что едет сюда, чтобы пристрелить меня. Бежать бессмысленно, да и поздно. Если он всерьез решил осуществить свою угрозу, то через 10 минут я буду мертв. Эта запись поможет полиции найти убийцу. Я слышу его шаги на лестнице. Дверь открывается…» На этом запись прервалась, Бонс выключил магнитофон.
— Может, арестовать Смита? — спросил лейтенант Вонг, помощник капитана Бонса.
— Нет, — отрезал Бонс. — Убежден, что убийство совершил кто-то другой, кто умеет хорошо подражать голосу Джонса. Запись сделана специально для того, чтобы направить расследование по ложному пути.
Как показали последующие события, Бонс был прав. Что заставило его заподозрить что здесь что-то не то?
35. В двух кошельках лежат 4 монеты, причем в одном кошельке монет вдвое больше, чем в другом. Как так может быть?
36. Есть куча кирпичей (считаем, что все одинаковые). У вас есть обычная линейка. Как за один замер определить диагональ кирпича?
P.S. Длина линейки достаточна. Диагональ не поверхности, а насквозь, например: от нижнего левого угла до правого верхнего угла другой стороны.
37. Один медведь решил начать путешествие. Он прошел километр на юг, потом повернул направо и прошел километр на запад, потом повернул еще направо, прошел километр на север. Оказалось, что он пришел туда, откуда начинал путешествие. Какого цвета медведь?
38. В одной тюрьме на всемирный день зэков устроили конкурс-игру. В игре участвуют все заключенные и в случае выигрыша администрация обещает всех их выпустить. Вот в чем заключается игра:
Всех заключенных сажают отдельно по разным карцерам. Затем одного любого из заключенных выпускают и ведут в специальный карцер с лампочкой. Никто из заключенных не знает и не может подсмотреть кого именно в тот карцер ведут. В специальном карцере есть 1 лампочка и заключенный имеет право включить/выключить/оставить без изменений лампочку. Затем его снова запирают в его карцере и берут произвольного другого заключенного (это может быть и тот самый).
Так игра продолжается целый день. Заключенные выигрывают если какой-то из заключенных выйдет из специального карцера и скажет «здесь уже были все заключенные» и это будет правдой, иначе, если это неправда, игра заканчивается.
Перед началом игры заключенные могут обсудить между собой стратегию игры, но во время игры никто ни с кем не может общаться. В начале лампочка выключена.
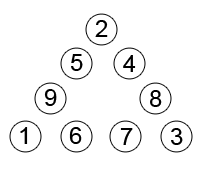
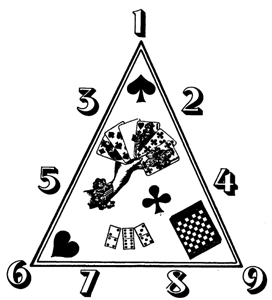
Задачка целиком на логику, не имеет никаких приколов типа оставить какой-то знак в спецкарцере, или на ощупь определить сколько работает лампочка…
Помогите заключенным выбраться из тюрьмы!
39. Во время летнего пикника четыре супружеские пары выпили 32 бутылки лимонада. Жены выпили: Жанна — 1 бутылку, Жаклин — 2 бутылки, Колета — 3 бутылки и Анета — 4 бутылки. Мужья не уступили женам: месье Пон выпил столько же, сколько его жена, месье Дюбуа — вдвое больше своей жены, месье Пейзан — втрое и месье Фонтен — вчетверо больше своих жен.
Как зовут мадам Пон, Дюбуа, Пейзан и Фонтен?
40. Эта задача известна с давних времен. Во вьетнамских деревнях старики-рисовщики любят задавать ее молодежи. Так задача переходит от поколения к поколению.
Для кормления 100 буйволов заготовили 100 охапок сена.
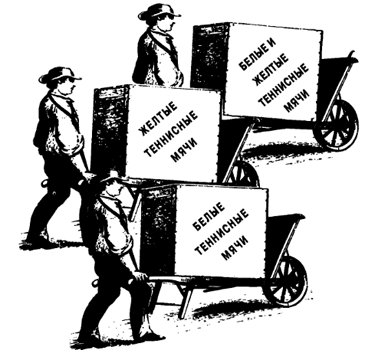
Молодой стоящий буйвол съедает 5 охапок сена.
Лежачий молодой буйвол съедает 3 охапки сена.
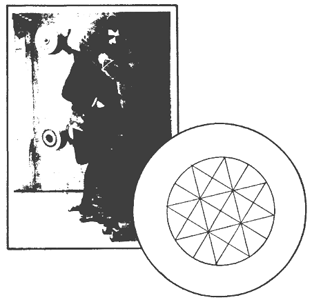
Старые буйволы втроем съедают 1 охапку сена.
Сколько молодых буйволов стоит, сколько лежат и сколько буйволов старых?
41. На обочине шоссе стоят километровые столбы. Шоссе ведет из пункта A в пункт В. На каждом столбе указано расстояние в километрах как от пункта А, так и от пункта В. Расстояние от A до В составляет 999 км. На скольких километровых столбах для обеих надписей использованы только 2 разные цифры?
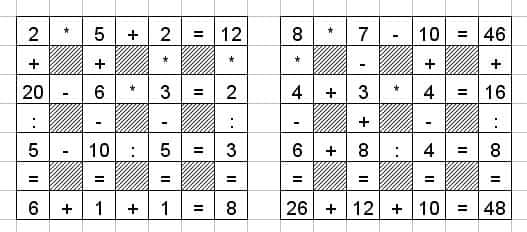
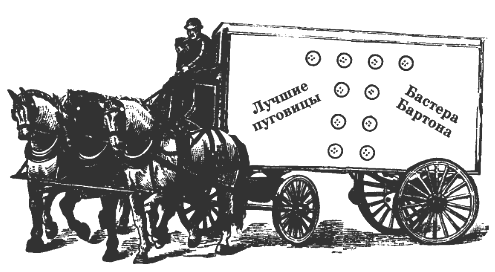
42. Расставьте числа (в рамке слева) и знаки арифметических действий (в рамке справа) так, чтобы в каждой строке получились правильно решенные арифметические примеры.
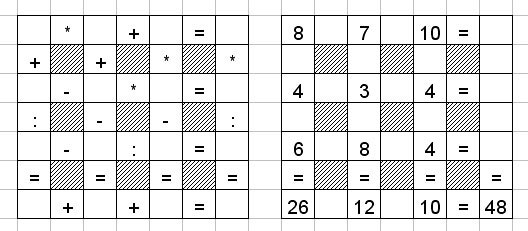
43. Отец по имени Николай с сыном и отец по имени Петр с сыном отправились ловить рыбу. Число рыб, пойманных Николаем, кончается на 2, а число рыб, пойманных его сыном, — на 3, число рыб, пойманных Петром, также кончается на 3, а число рыб, пойманных его сыном,- на 4. Число рыб, пойманных нашими рыбаками вместе, совпадает с квадратом некоторого натурального числа. Как зовут сына Николая?
44. Рыбаки Адам, Бауэр, Кристиансен и Дазе (сокращенно А, В, С и D — по первым латинским буквам их имен), взвесив свой улов, установили следующее:
(1) D поймал больше, чем С.
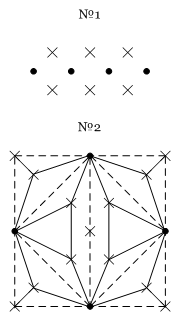
(2) А и В вместе поймали столько же, сколько С и D (вместе).
(3) A и D вместе поймали меньше, чем В и С (вместе).
Расположите результаты взвешиваний уловов а, b , с и d . рыбаков A, В, С и D по величине.
45. Учитель начертил на классной доске четырехугольник. Янош утверждал, что это квадрат. Имре считал, что четырехугольник — трапеция. Мария думала, что на доске изображен ромб. Эва назвала четырехугольник параллелограммом. Выслушав каждого и подробно изучив свойства четырехугольника, учитель установил, что ровно 3 из 4 утверждений верны и ровно 1 утверждение ложное. Какой четырехугольник начертил учитель на классной доске?
46. Найти трехзначные числа вида аЬс, цифры которых удовлетворяют уравнению a² — b² — с² = а — b — с (все 3 цифры числа должны быть разные).
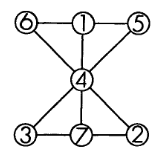
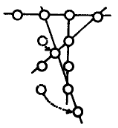
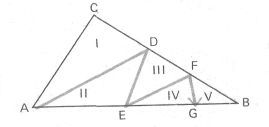
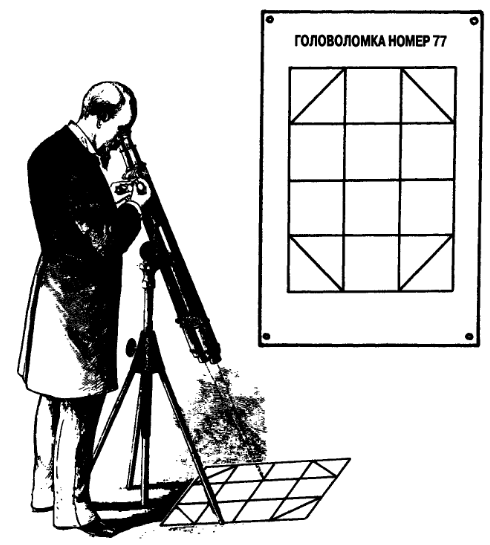
47. «Подальше положишь — ближе возьмешь». Перед нами хитрый крот. Между своей спальней А и выходом Е он проложил хитроумную систему ходов и камер. Каждое утро крот идет из Е в А и по дороге проходит через свою запасную кладовую. Интересно, что отыскивает он ее по определенному правилу. Если крот достигает выхода Е, миновав 3, 5, 7, 9 или 11 промежуточных остановок (обозначенных на плане кружками), то кладовая остается в стороне. Если же крот добирается до выхода Е после четного числа промежуточных остановок, то по пути он непременно наталкивается на запасную кладовую. Между какими двумя камерами расположена запасная кладовая хитрого крота?
48. Эта загадка на сообразительность для детей. А вы сможете ее решить?
8809 = 6
7111 = 0
2172 = 0
6666 = 4
1111 = 0
3213 = 0
7662 = 2
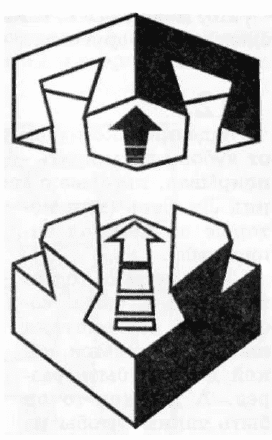
9312 = 1
0000 = 4
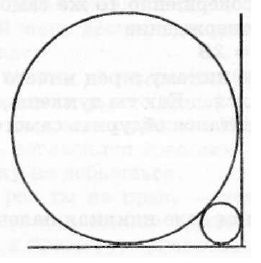
2222 = 0
3333 = 0
5555 = 0
8193 = 3
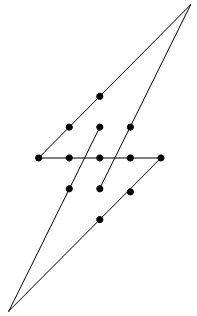
8096 = 5
7777 = 0
9999 = 4
7756 = 1
6855 = 3
9881 = 5
5531 = 0
2581 = ?
49. Джон Харрис из г. Санта-Барбара изобрел новую игру. «Путешествие перекатывающейся игральной кости». Для того чтобы нам легче было следить за маршрутом игральной кости, покрасим одну из ее граней в какой-нибудь цвет. С одного поля шахматной доски на соседнее игральная кость «путешествует», перекатываясь через ребро, соединённое с общей стороной этих двух полей.
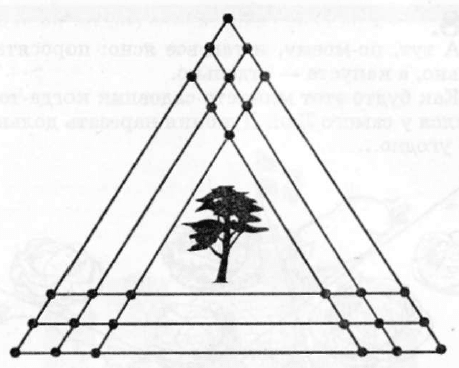
А теперь решим задачу.
Поставьте игральную кость на левое верхнее поле шахматной доски цветной гранью вверх. Можете ли вы указать маршрут, «путешествуя» по которому, игральная кость побывает по одному разу на всех полях шахматной доски и окажется в правом верхнем углу цветной гранью вверх? Во время путешествия из угла в угол цветная грань игральной кости (так говорят правила игры) нигде, кроме начального и конечного поля, не должна быть расположена вверх.

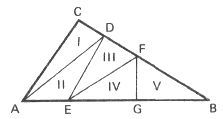
50. Разделить заданный треугольник с помощью зигзагообразной ломаной на 5 равновеликих частей.
51. Цепь из 15 звеньев порвали на 5 частей. Как ее соединить за 6 действий.
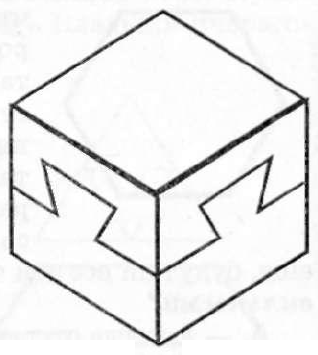
52. Драгоценный клад лежит в шкатулке с очень необычным замком: шипы на его стенках плотно цеплялись друг за друга (смотрите рисунок). Открыть его можно, догадайтесь как?
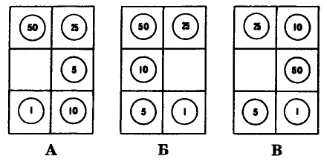
53. Пингвины, которых вы видите на рисунке, решили загадать вам непростую загадку.
Расставьте их так, чтобы сумма проставленных чисел в горизонтальных и вертикальных рядах, а так же по диагонали составляла 12.

54. Похоже, что остальные участники ежегодного конкурса головоломок не очень обрадовались этому сообщению. В головоломке, изображенной на рисунке, нужно было определить четыре следующие цифры в ряду представленных чисел. Держите носовой платок наготове — в вашем распоряжении всего пять минут!

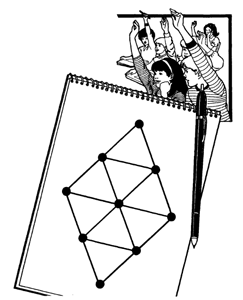
55. Дети на рисунке знают решение этой математической задачи. Геометрическая фигура в блокноте состоит из восьми треугольников, образованных шестнадцатью отрезками. Необходимо передвинуть четыре отрезка так, чтобы получилось четыре треугольника одинакового размера. В вашем распоряжении пять минут.
56. Молодая художница выиграла соревнование за право нарисовать победителя грандиозного конкурса головоломок. Она и не подозревала, что ее работа так же окажется головоломной. Однако художница не только прекрасно написала портрет, но и решила головоломку. Набрав на кисть побольше краски, девушка одним движением нарисовала то, что вы видите. Она ни разу не пересекла собственную линию. А вы так можете?

57. На рисунке — талисман знаменитого картежника Джорджа Веллингтона-Толстосума. К сожалению, художник перепутал порядок цифр, и талисман потерял силу. Чтобы ее восстановить, вы должны расставить цифры от единицы до девяти таким образом, чтобы их сумма на каждой стороне треугольника равнялась 17. Цифры на углах, разумеется, так же учитываются.
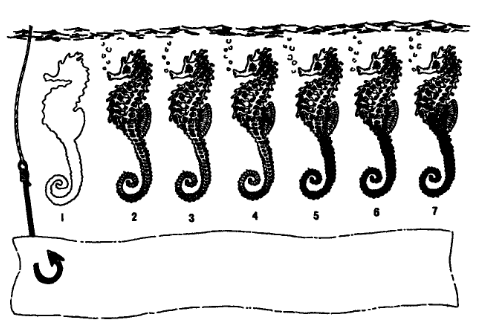
58. Шесть веселых морских коньков выстроились в ряд, чтобы сыграть в одну игру. У первых трех — светлые хвосты, а у трех последних — темные. Цель игры — поменяться местами не более чем за десять ходов. Морской конек может делать один ход назад или вперед, если соседнее место рядом с ним свободно, или переплывать над одним или двумя коньками, чтобы занять свободное место. В конце игры три первых места должны быть заняты морскими коньками с темными хвостами, следующие три — со светлыми хвостами, а седьмое место должно остаться свободным.
Это задание кажется простым, но смотрите, не попадитесь на крючок.
59. Сэр Роджер не только выглядит щеголем, но и имеет репутацию отличного фехтовальщика. Однажды рано утром, собираясь на очередную дуэль, которых было так много в его жизни, он искал пару чулок одного цвета. Сэр Роджер знал, что в нижнем ящике гардероба лежат десять пар белых чулок и десять пар черных, но свет единственной свечи был таким тусклым, что он не мог разобрать цвета. Определите минимальное количество чулок, которое должен извлечь из ящика сэр Роджер, чтобы подобрать пару одинаковых.
60. Итак, внимание! Любимая учительница 5-й мужской гимназии миссис Присцилла Норт предлагает решить математическую задачку, и к тому же нелегкую.
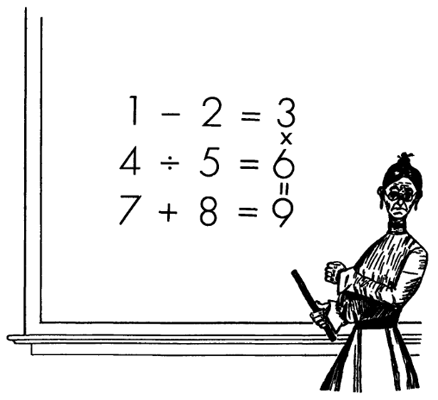
— Я написала очень интересное уравнение. Но, к сожалению для вас, расположила цифры от единицы до девяти в неправильном порядке. Вы должны переставить их так, чтобы все четыре примера имели правильное решение.
Имейте в виду: здесь три «горизонтальных» уравнения и одно «вертикальное».
61. Этот маленький старый часовщик хочет проверить вашу наблюдательность и внимательность. Он выставил в витрине девять замечательных часов и предлагает вам расставить их в десять рядов по трое часов в каждом. Вы будете просто молодцом, если справитесь менее чем за пятнадцать минут!

62. Неутомимые археологи Хопкинс и Паркер откопали очередной древний памятник. Давайте послушаем, о чем они говорят:
— Наконец-то и мы сделали сенсационную археологическую находку — обнаружили текст знаменитой «Загадки Сфинкса»! Ей не менее трех с половиной тысяч лет!
— Что значит «мы»? — ехидно прошипел Хопкинс. — Я тут ни при чем! Хотел бы я посмотреть на древнего египтянина, выбивающего на камне буквы неизвестного ему языка.
Разумеется, этот памятник — подделка, но загадка сама по себе неплохая. Попробуйте ее разгадать, пока Хопкинс и Паркер спорят о прошлом.

63. Однажды великий Сэм Купер, владелец спортивного магазина «Мячи и Ракетки», проверял новую партию теннисных мячей. Вдруг он заметил, что на трех ящиках неправильно наклеены этикетки. Будучи известным любителем головоломок, он увидел в этой ситуации прекрасную возможность поломать голову. Вот условия этой головоломки.
Возьмите один теннисный мяч из любого ящика, не заглядывая ни в него, ни в другие ящики. Зная цвет только одного теннисного мяча, определите, какие должны быть этикетки на каждом из этих ящиков.
Попробуйте решить задачу за десять минут. Использовать дополнительное время не разрешается.
64. Здесь, в центре этой ужасной пустыни, находится затерянный город Иштар. Чтобы до него добраться, я должен идти пешком от побережья до центра материка. Двигаясь по этой дороге, человек может взять с собой запасов продовольствия не более чем на пять дней. Я подсчитал, что могу продвигаться за день самое большее на тридцать миль. Судя по карте, город находится на расстоянии ста двадцати миль от побережья. Сейчас я попробую подсчитать, сколько нужно людей, включая меня самого, чтобы хватило запасов на одного для того, чтобы добраться до города, переночевать там и вернуться на побережье.

65. Этот сияющий джентльмен явно доволен своим новым приобретением. Но все же чей портрет он рассматривает? Каковы отношения между этим ценителем искусства и изображенным на картине?

66. На востоке один старик, умирая, завещал трем своим сыновьям 19 верблюдов. Старшему сыну по завещанию должна была достаться половина верблюдов, среднему — четверть, и младшему — пятая часть. Но братья стали спорить между собой, ведь 19 верблюдов не делится, ни на 3, ни на 4, ни на 5. Пошли они к мудрецу, у которого тоже были верблюды. И мудрец смог рассудить их, и вроде бы каждый остался при своей доле.
Как разделил верблюдов мудрец?
67. Какие вопросы (не более 10) нужно задать человеку, загадавшему число от 1 до 1000, чтобы получая на них только ответы «да» и «нет» отгадать это число.
68. Сто лет назад не было пуговиц лучше, чем пуговицы Бастера Бартона. На рисунке — фургон, на котором пуговицы развозили по магазинам. Уже тогда кто-то заметил, что узор из пуговиц на фургоне представляет собой головоломку. Десять пуговиц расположены в три ряда по четыре пуговицы в каждом ряду (один горизонтальный ряд и два вертикальных). Передвинув всего две пуговицы, попробуйте составить четыре ряда по четыре пуговицы в каждом ряду. На это задание вам выделяется десять минут.
69. Перед вами — настоящий тест на проверку интеллекта. На рисунке изображены шесть произвольно расположенных кругов, треугольников и квадратов. Ваша задача — назвать остальные три фигуры в каждом ряду.
Подумайте хорошенько и беритесь за карандаш.

70. Этой замечательной задаче уже более ста лет. На рисунке вы видите шестнадцать карт, разложенных в четыре ряда по четыре карты в каждом ряду. А теперь переложите карты таким образом, чтобы в каждом ряду по горизонтали, по вертикали и по диагонали не было двух карт, одинаковых по значению или масти.

71. Ограбление оптового склада стало для Вилли, знаменитого взломщика сейфов, очень выгодным делом. Ему повезло с самого начала, когда он купил полный план всех этажей здания. К сожалению, в плане не было указано, как выглядит склад, который он собирался ограбить. Вилли выяснил, что склад — квадратной формы, а большая комната имеет выход на улицу. Четыре маленькие комнаты выходят в большую комнату. В пятой находится заветный сейф. Для получения полного плана Вилли просто провел четыре прямые линии в квадрате, изображенном на рисунке. Как он провел эти линии?

72. Мерлин, великий и мудрый волшебник при дворе короля Артура, любил следующую загадку: выберите четыре монетки и расположите их таким образом, чтобы все они были на равном расстоянии друг от друга. (Если у вас под рукой нет английских монеток, подойдут любые другие).
73. Эти братья-курильщики не разговаривают друг с другом с тех пор, как Бертрам выиграл у Августа шахматную партию. До этой черной пятницы Бертрам ни разу не выигрывал у брата. Вот как это произошло:
— Август, готов побиться с тобой о залог на коробку твоего любимого табака, что, если мы с тобой одновременно будем играть две шахматные партии, я либо выиграю одну из них, либо сведу обе вничью. Единственное мое условие — играть на двух разных досках, причем на одной я буду играть черными, а на другой — белыми. Кроме того, чтобы у тебя не было сомнений в моей честности, я уступаю тебе право первого хода. Сыграем?
Каким образом Бертраму удалось добиться победы?
74. Известный фермер Джон Коу имел репутацию довольно эксцентричного джентльмена. Составляя план постройки новых загонов для своих девяти телок-рекордсменок, он велел своим работникам построить четыре загона, причем в каждом из них должно располагаться нечетное количество животных. Интересно, удалось ли работникам выполнить условие придирчивого хозяина?

75. Пилигрим Томас Тинкер придумал эту головоломку в день основания колонии Плимут. Ежегодно там проводится конкурс на лучший торт! А теперь попробуйте тремя движениями большого ножа разрезать торт-победитель на восемь равных кусков. Желаем удачи!

76. Вилли-Ковзаняр стал победителем Бала Головоломных Роллеров в 1889 году. Вот он — на рисунке — с главным призом. Рядом — свидетельство его непревзойденного умения придумывать головоломки. Он сумел точно воспроизвести рисунок, который вы видите, потратив на это рекордно мало движений.
Попробуйте, не отрывая карандаша от листа, определить, сколько ходов сделал Вилли, чтобы выиграть желаемый приз. Каждый раз, когда карандаш меняет направление движения, считается за один ход. Внешний круг также считается за один ход. Разрешается иногда проходить карандашом по одному и тому же месту более одного раза.
77. На рисунке изображен профессор Скептикер, проверяющий ответ победителя прошлогоднего Международного конкурса головоломок. Профессор удостоверился, что в головоломке номер 77 никакие линии не пересекаются. Чтобы проверить самого профессора, начертите изображенную здесь фигуру, не отрывая карандаша от бумаги. Линия нигде не должна пересекаться. Нельзя также сгибать лист.
78. Мистер Уильямс, мистер Барнет и мистер Эдвардс живут в меблированных комнатах на Баскет-Стрит. Один из них — пекарь, другой — таксист, а третий — пожарный. Вы должны определить профессию каждого из них. Вот несколько подсказок.
1. Мистер Уильямс и мистер Барнет каждый вечер играют в шахматы.
2. Мистер Барнет и мистер Эдвардс вместе ходят на бейсбол.
3. Таксист собирает коллекцию монет, пожарный — оловянных солдатиков, а пекарь — марки.
4. Таксист никогда не ходит на бейсбол.
5. Мистер Эдвардс никогда не слышал о почтовых штемпелях.

79. Дверь официанта расположена в углу зала. Нарисуй маршрут официанта так, чтобы он прошел через все столики и вернулся к своей двери. Но он не может ходить по диагонали и проходить дважды по одному месту. В зале стоят 3 колонны, которые, как понятно, нужно обходить.

80. Это одна из тех головоломок с перестановками, которые мы все так любим (ведь любовь зла, не так ли?). Сначала положите три монетки на черные круги в квадратах 2, 3 и 4, затем положите три монетки на белые круги в квадратах 5, 6 и 7. Теперь за семь ходов поменяйте монетки местами, передвигая их с одного квадрата на другой по черным линиям, которые соединяют квадраты. При этом можно передвигать монетку только на пустые квадраты.
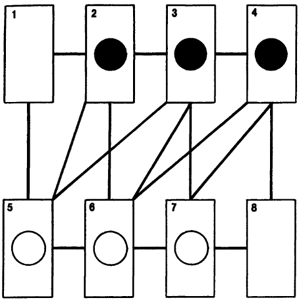
81. Как-то раз Шалтай-Болтай позвал каменщика и попросил его построить у себя в саду две кирпичные стены одинаковой высоты и длины (на рисунке расстояние между буквами А и Б равно расстоянию между В и Г). Каменщик ответил, что за стену ВГ он возьмет больше денег, потому что ее надо возводить на холме и для нее потребуется больше кирпича. — Ерунда, — сказал Шалтай-Болтай. — Она будет стоить дешевле, потому что для нее понадобиться меньше кирпичей и строительного раствора. Как вы думаете, кто из них прав?

82. Для решения этой интересной задачки вам нужно сделать увеличенную копию этого рисунка и взять восемь шашек, которые послужат фишками. А теперь разместите шашки на линиях рисунка так, чтобы в каждом круге и на каждой из четырех прямых линий было по две шашки.

83. Сделайте такое же игровое поле, разделите его на шесть частей и разместите на поле монеты в пол доллара, четверть доллара, десять центов, пять центов и цент. Передвигайте за один ход по одной монетке, поменяйте местами пол доллара и цент. Разрешается двигать монеты только по горизонтали или вертикали.
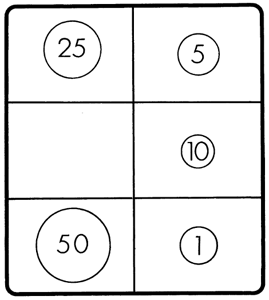
84. Перед вами доблестный страж во время выполнения служебных обязанностей — охраны королевских регалий Англии. Этот сильный малый часами стоит на посту, созерцая самую богатую в мире коллекцию. В один прекрасный день, стоя перед витриной с двенадцатью коронами, Херолд впал (минут на десять, не больше) в гипнотический транс и выйдя из него с удивлением обнаружил, что приобрел дар составления головоломок! Итак, можно ли соединить двенадцать корон пятью прямыми линиями так, чтобы каждая из них продолжала следующую, а все вместе они образовывали замкнутую фигуру? На решение этой головоломки даем вам десять минут, а победитель заслуживает титул «Король головоломок».

85. Ну, раз уж мы вернулись к монетам, то почему бы не поломать голову и над этой задачкой? Итак, попробуйте расположить на 16 клетках четыре монеты одного номинала и четыре другого так, чтобы ни в одном ряду — горизонтальном, вертикальном или диагональном — не встречалось бы по две одинаковые монеты. Будьте внимательны — эта задачка не так проста, как кажется!

86. В 1876 году французский изобретатель и художник Эмиль Рено, приложивший усилия к созданию мультипликационного кино, изобрел праксиноскоп — аппарат для рассматривания движущихся изображений. Вы видите профессора во время демонстрации головоломки «Загадочный предмет». На экране сверху проекция предмета спереди, а снизу — его вид сбоку. Профессор Рено предлагает присутствующим определить по двум проекциям форму предмета в трёхмерном изображении. Не желаете присоединиться?

87. — Поздравляю с удачным приобретением! Отличная садовая скульптура! А кто же скульптор?
— Кто скульптор? Сам Газ Сварк! Правда, работа еще не закончена. По замыслу автора, композицию свяжут воедино три прямых прута. Только он никак не может взять в толк, как их приварить в скульптуре, чтобы они пересекли все квадраты по одному разу…
Может, вы подскажете гению металлоскульптуры?

88. Под низким мостом остановился грузовик. Его нельзя было подвинуть вперед, не повредив крышу. Что бы проехать, не хватало каких-то 3-х сантиметров. Шофер грузовика пребывал в полном недоумении, пока маленькая девочка не предложила ему простое решение.
Какое?
89. У мальчика столько же сестер, сколько и братьев, а у его сестры сестер в два раза меньше, чем братьев. Сколько в семье сестер и братьев?
90. Когда мы смотрим на цифру 2, а говорим 10?
91. В записи *1*2*4*8*16*32*64=27 вместо знаков «*» поставьте знаки «+» или «-» так, чтобы равенство стало верным.
92. Зачеркните все 13 точек (как на рисунке) пятью отрезками, не отрывая карандаша от бумаги и не проводя никакую линию дважды.

93. Чтобы найти пиратский клад надо пройти от старого дуба 12 шагов на север и 5 шагов на юг, затем 4 на север и 11 на юг. Где зарыт клад?
94. На одном берегу реки стоят четыре человека, а у берега пришвартована лодка. Всем им нужно переправиться на другой берег реки. Известно, что один из них может переправится за 1 час, второй за 2 часа, третий за 5 часов, а четвертый за 10 часов. В лодку могут поместиться одновременно не более 2х человек. Если в лодке находятся двое, то время переправы следует считать так как будто переправлялся тот, чье время переправы дольше. Переправится нужно всем не более чем за 18 часов. Лодка сама не перемещается с берега на берег, в ней должен кто-то быть.
Как им поступить?
95. У одного садовника есть 10 деревьев. Ему нужно их высадить в 5 рядов таким образом, что бы в каждом ряду было по 4 дерева. Как он должен высадить деревья?
96. Какой знак надо поставить между написанными рядом цифрами 2 и 3, так чтобы получилось число, больше двух, но меньше трех?
97. Кузнечик прыгает вдоль прямой вперед на 80 см или назад на 50 см. Может ли он менее чем за 7 прыжков удалиться от начальной точки ровно на 1 м 70 см?
98. Вы находитесь в центре круглого озера, радиусом R. По берегу озера бегает очень умный гоблин. Он бегает со скоростью в 4 раза больше, чем вы плаваете. Но если вы выберетесь на берег, а его там еще не будет, то вы сможете от него убежать. Сложность в том, что это очень умный гоблин, и он способен предугадать все ваши ухищрения, и он всегда действует логично.
Как вам убежать от этого гоблина и выбраться из озера?
99. Дед позвал внука к себе в деревню: «Вот посмотри, какой я необыкновенный сад посадил! У меня там растет четыре груши, а еще есть яблони, причем они посажены так, что на расстоянии 10 метров от каждой яблони растет ровно две груши». — «Ну и что тут интересного, — ответил внук. — У тебя всего две яблони». «А вот и не угадал, — улыбнулся дед. — Яблонь у меня в саду больше, чем груш». Нарисуйте, как могли расти яблони и груши в саду у деда. Постарайтесь разместить на рисунке как можно больше яблонь, не нарушая условий. Если Вы думаете, что разместили максимально возможное число яблонь, попробуйте объяснить, почему это так.
100. Священный жук Скарабей неутомимо скатывает шарики — из всего, что попадется ему на пути. И если встретится ему другой Скарабей (не такой уж и священный, потому что у него шарик поменьше), то и его самого, и его шарик закатает большой Скарабей в свой шар. Как спастись маленькому жуку, если большой уже почти загнал его в угол?
101. В саду растет 27 дубов так, как показано на рисунке. Нужно пересадить их так, чтобы все 27 дубков стояли снова в 9 рядов по 6 деревьев в каждом — и ни одного дубка в стороне.
102. Сумма каких двух натуральных чисел равна их произведению?
Возможно вам будет интересно: